planetshape

The Shapes of Planets

The fundamental shapes of nature

Introduction

Planetary scientists describe the shapes of planets using an "alphabet" of shapes. These are the same shapes that appear in the orbitals of an electron around hydrogen. They are known as spherical Legendre Polynomials.

These shapes are all shapes which can be drawn flat on a piece of paper, the full three dimensional shape of the planet is created by rotating them about a vertical line.
Thus the first shape below is drawn as a circle, the spherical shape of the planet is created by rotating the circle about a vertical line through its center.

The Sphere

Think of photos of the earth you have seen from space.
The fully illuminated earth looks like a sphere.

That is because the earth and most other planets are very good approximations to spheres.

So the first fundamental shape of a planet is spherical.

The zeroth spherical harmonic, the sphere.

The zeroth legendre polynomial is very simple P0(q) = 1
(Which, when you think about it, is a mighty strange way to write 1.)

The equation for a sphere in spherical coordinates is r = J0 P0(q).
The radius, r, is a constant, J0 times 1.

The earth is a sphere with an average radius of approximately 6,368 km.
So J0 = 6368 km

This is the same shape as the 1s orbital in hydrogen but on a different size scale.

Offset center of mass.

The Moon is nearly spherical.
However, if you draw a sphere which neatly fits the moon the center of the sphere is displaced from the center of mass of the moon.

The center of mass of the moon is offset from the center of its figure.

The center of mass of the moon is offset from its so called center of figure by 2 km.

The offset is partly due to the Moon's very different two sides. The side of the moon that faces the earth is covered by dense dark basalt of the lunar mare. The farside of the moon has few mare, yet is covered with less dense, light-colored highland rock. This causes the offset in the center of mass toward the earth.

Many solid planets have this two-sided nature. Mars for instance, has the southern half of its surface covered with heavily cratered terrain while the other half is covered with sparsely cratered lava flows.

The equation for a pure offset uses the first legendre polynomial

P1(q) = sin q

Then r = J0 P0(q) + J1 P1(q), where q is the angle measured from the north pole.

Now P1(q) = sin q

The shape of the moon is the sum of a spherical term and a smaller offset term.

Where J0 is the radius of the moon , 1238 km

and J1 is the center of mass offset, 2 km

So at q = 90 which is on the equator, to the right of the above illustration, the radius of the surface is largest and equal to r = J0 +J1, while at q = 270, sin q = -1, and the surface has a radius of r = J0 + J1.

Equatorial Bulge

The radius of the earth at the equator is greater than the radius of the earth at the poles.

The earth has an equatorial bulge. (See the Spin a Koosh activity.)

The equatorial bulge of the earth is 21 km, about 0.3% of its radius.

The equatorial bulge of the earth can be created by adding the second spherical harmonic to the earth's basic sphere.

The second spherical harmonic looks like a figure 8.

The second harmonic looks like a figure 8

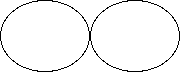
This is the 2p orbital for hydrogen.

The equation for this spherical harmonic is P2(q) = (3 sin²q -1)/2.

The radius is zero at the poles and increases to a radius of 1 at the equator.

The earth's shape is created by adding the second harmonic to its basic spherical shape:

r = J0 + J1 P1 + J2 P2

If we divide every term by the radius we get:

where J0 = 6368 km, J1 = 0 km, and J2 = 21 km.

You cannot see the difference from a spherical shape for this small of an equatorial bulge.
Factoring out the radius we get

r = J0( 1 + J1/J0 P1 + J2/J0 P2)

Where, for the earth, J0 = 6368 km, J1 = 0 and J2/J0 = 0.003%

However, Jupiter has an equatorial bulge which is 7% of its radius, J2/J0 = 0.07.
Factoring out the radius of Jupiter its equation is:

r = J0 (1 + J2/J0 * (P2(q))

with J0 = Rj = 71,492 km at the equator.

Here is an illustration of the equatorial bulge of Jupiter.

Jupiter with its 7% equatorial bulge.

Etc

Isaac Newton predicted that the earth would have an equatorial bulge, French astronomers of the Cassini family analyzed the first measurements and found that the earth bulged out at the poles and contract around the equator. Teams were dispatched by the French to measure the shape of the earth more acurately. These repeated measurements showed that Isaac Newton was correct.

Etc.

The tallest mountain on earth measured from sea level is Mt. Everest, however the tallest mountain on earth measured from the center of the earth is the Ecuadorian peak Chimborazo. This is because Chimborazo is closer to the equator than Everest and so sits higher up on the earth's 21 km high equatorial bulge.

The Pear Shape of the earth

The first satellites measured the shape of the earth's sea level.

They discovered a small pear shape.

This is the third harmonic term. P3(q) = (5sin³q - 3 sin q)/2

r = J0 (1 + J1/J0 P1(q) + J2/J0 P2(q) + J3/J0 P3(q))

J3 is 1000 times smaller than the equatorial bulge, with a height of about 10 m.

The pear shape pokes up at the north pole and dimples in the south.

You can not see the pear shape of the earth at all unless you ignore the equatorial bulge and greatly exaggerate the amplitude of the pear shape.

Saturn and the fourth harmonic

Saturn has a fourth harmonic added to its sphericity and equatorial bulge.

This is the shape of one of the 3d orbitals of hydrogen.

And Beyond

The shape of the earth has been found by orbiting satellites up beyond the 320'th spherical legendre polynomial.

The Spherical Legendre Polynomials

The polynomals have these funny forms so that they will be normalized and so that they will be orthogonal to each other.