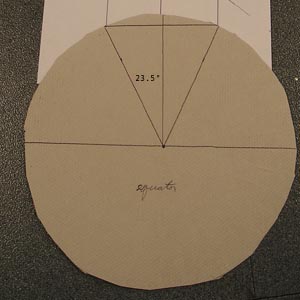
On a circular disk an arc of 23.5 degrees from east to solstice sunrise defines a semichord.
The straight lines above the disk show the paths of sunrise viewed from the equator.
Derivation of the angle of Solstice sunrise versus latitude.
Introduction
The equation of spherical geometry that is used to calculate the angle between east and the direction of solstice sunrise can be derived using scissors, rulers and paper plates.
Material
To Do and Notice
Use the compass to trace a large circle in the middle of each paper plate.
Make sure you mark the center of each circle.
Label on paper plate "Equator."
Draw an east-west line on this paper plate passing through the center.
Draw a line from the center making an angle of 23.5 degrees with respect to the east-west line. Then draw a second line 23.5 degrees on the opposite side of the east-west line. (Use a protractor to create the correct angle.)
If this plate were placed on level ground at the equator with the center line running east-west, the sun would rise on the east-west line on the equinoxes and on the 23.5 degree lines at the solstices.
Draw a line between the points where the 23.5 degree lines meet the circumference of the circle. The length of this line is R * sin(23.5) = sin(23.5) where R is the radius of the disk, choose R = 1.

As an observer moves away from the equator towards higher latitudes, L, the sun appears to rise into the sky along lines that are tipped at an angle L away from the vertical. For example, at L = 10 degrees latitude the sun rises on a line tipped 10 degrees from the vertical. And at L = 38 degrees latitude the sun rises on a line tipped 38 degrees from the vertical. The distance along the horizon between the solstice lines is given by the perpendicular distance between the solstice lines divided by the cosine of the latitude.

At latitudes north of the equator the distance along the horizon between the equinox sunrises and the solstice sunrises increases. Because the distance between the parallel lines of the suns motion increases when the distance is measured along a line that is not perpendicular to the parallel lines.
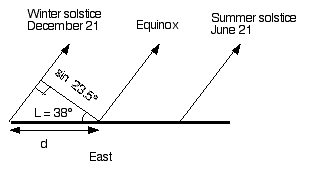
In the above drawing notice the right triangle The relationship between d, the distance along the horizon and the sin(23.5) is given by the cosine.
Cos (L) = sin(23.5)/d
so d = sin(23.5)/cos(L)
Now in the final step we can convert the semichord d back to an angle, D. Where D is the angle between the east-west equinox sunrise and the solstice sunrises.

Use the second disk.
Draw an east west line as a diameter of the disk.
Mark a chord of length 2 * d on the disk. Draw lines from the center of the disk to each end of the chord.
Measure the angle, D, between the east-west line and one of these lines.
Notice that the sin of this angle is Sin (D) = sin (23.5)/Cos (L)
Try this construction for your latitude. The illustrations above were for the latitude of San Francisco. L = 38°. The angle D was 30 degrees.
|
Scientific Explorations with Paul Doherty |
|
14 May 2005 |