
An image of the 1882 transit. courtesy of Lick Observatory. Photography had not been invented in 1761.
Transit of Venus and the Astronomical Unit
A Math Root developed by Paul Doherty

An image of the 1882 transit. courtesy of Lick Observatory. Photography had not been invented in 1761.
In 1761 scientists traveled all over the globe to observe the transit of Venus. They hoped that their observations would lead to the calculation of the "Astronomical Unit" The average radius of the earth's orbit. By observing the position of a star against the distant background of stars twice half-a-year apart astronomers could construct a triangle with a base length equal to the astronomical unit. Thus the astronomical unit was the key distance used to determine the distances to stars and eventually the distance to the edge of the visible Universe.
In 1824 the calculations based on the observations observations were finally finished and scientists knew more accurately than ever before the distance from the earth to the sun.
Let's see how the astronomical unit can be calculated by observations of a transit.
The basic idea is to use triangulation. The transit of Venus is observed from two different latitudes on earth.
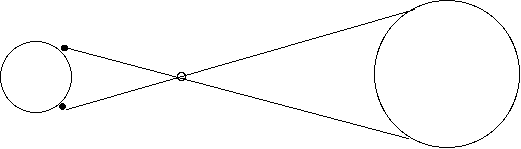
The Earth, Venus and the sun drawn horribly out of scale. Two observers on earth view the transit and see Venus located at different positions against the sun.
Consider two observers one at 45 degrees north latitude and one at 45 degrees south latitude, they are located on the same line of longitude. (For this calculation we'll ignore the angular tip of the earth's axis of 23.5 degrees.)
Assignment, find two observing points on earth that fit the above conditions.
(Note I'll do all calculations to 2 significant figures.)
Calculate the straight line distance, d, between these two points. You'll need to know that the radius of the earth is r = 6.4 x 106 m.
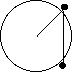
Calculate the straight line distance between two points on earth
at the same longitude and separated by 90 degrees of latitude.
Click here to see the geometry of the
answer.
The distance, d, is 9.0 x 106 m.
It was known in 1761 that Venus was 0.72 times as far from the sun on the average as was the earth. So astronomers knew the ratio of the distances but they did not know the actual distances. They knew this because of Kepler's laws. In particular Kepler's third law relates the radius of an orbit, R, to its period, T.
Kepler found that T 2/R3 = C where C was a constant throughout our solar systtem. Astronomers knew the period of earth's orbit and of Venus' orbit so they could calculate the relative radii of the orbits. T earth = 365.2 days, T Venus = 224.7 days set up a ratio given that R for earth is defined as 1 AU and calculate the R for Venus.
The path of Venus across the sun viewed from two different latitudes.
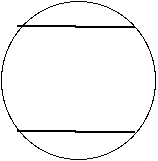
The path of Venus across the sun as viewed from two different latitudes on earth, greatly exagerated.
Pretend for the next few calculations that the two transit paths exist as black lines drawn across the face of the sun.
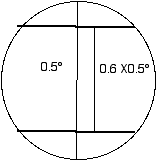
The sun subtends a half a degree, 0.5°, measured from the earth. If the path of Venus across the sun is 0.6 of the total diameter of the sun then the path of Venus subtends 0.6 * 0.5° = 0.3°.
If the two paths of the Venus transit were viewed from the center of the earth they would be separated by 0.3 degrees.
The actual angle of separation of the paths as viewed from earth is 0.018 of the angular diameter of the sun or 0.009 degrees.
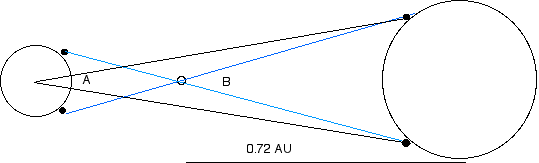
The angle A subtended by the two transit paths
(Each path was viewed from different point on earth.)
The angle B subtended by the two transit paths viewed from
Venus.
The angle between the two transit paths from Venus can be calculated from the angle between the transit paths viewed from earth. The center of the earth is 1 AU from the sun while the center of Venus is 0.72 AU from the sun so the, the angles are all small. So angle B = A/0.72 = 0.009/0.72 = 0.0.0125° or 0.00022 radians.
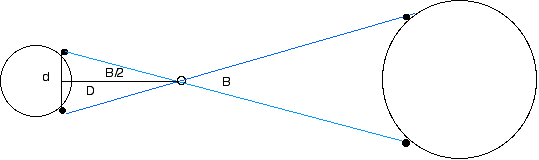
Tan (B/2) = (d/2)/D so D = (d/2)/ Tan (B/2)
Since the angle B is a small angle then Tan B = B if B is measured in radians.
Thus D = d/B = 9 x 106 m / 2.2 x 10-4 = 4.1 x 1010 m
We know that the distance from the earth to Venus is 0.28 AU so we can calculate the AU.
0.28 AU = 4.1 x 1010 m
1 AU = 4.1 x 1010 m / 0.28 = 1.5 x 1011 m
Which is close to the value for the AU obtained in 1824 and close to the currently accepted value.
Etc.
The current value for the astronomical unit can be obtained by bouncing radar signals off the surface of Venus.
A drawing showing how to calculate the distance
between two points on the surface of the earth.
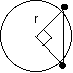
The points on the surface of the earth are on a 45-45-90 triangle
with one vertex at the center of the earth.
Thus the distance between the points is the hypotenuse of an isosceles right triangle and by the Pythagorean theorem is the square root of two times the length of one side. Thus the distance is 1.4 x 6.4 x 106 m = 9.0 x 106 m.
|
Scientific Explorations with Paul Doherty |
|
1 May 2004 |