drop_a_slinky

Drop a Slinky

Falling faster than g

Introduction

Hold a slinky by its top end, then drop it.
The top accelerates downward faster than g.

Material

A plastic slinky
A heavy object (such as a hacky sack, or film can, or set of keys)
scissors to cut the sliny.

Assembly

Cut the slinky so that it hangs about 1/2 way to the floor when you hold its top as high as possible.

To Do and Notice

Hold the slinky by its top and drop it several times.
Notice how it pulls together as it falls.

Hold the ball next to the top of the slinky and drop both at the same time.
Notice how the top of the slinky drops faster than the ball.

Hold the ball next to the bottom of the slinky and drop them both together.
Notice how the bottom of the slinky falls slower than the ball.

Drop the ball next to the center of mass of the slinky.
Notice that the ball and center of mass fall together.
To find the center of mass of the slinky, compress the slinky so that all of its coils are together. Then mark the center coil with tape or a pen.

Notice that when the slinky is stretched out under gravity the center of mass mark is not at the center of the slinky.

What’s Going On?

Regardless of their mass, in the absence of air resistance all objects accelerate toward the earth at the acceleration of gravity,g.
For an extended object like a stretched slinky, the center of mass accelerates downward at g. Parts of the slinky accelerating with respect to the center of mass accelerate faster or slower than g.

Consider the top slink of the slinky.
When you hold it stationary.
Your hand is pulling it up. The rest of the slinky is a stretched spring pulling it down. Gravity is pulling it down.

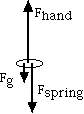
The forces on the top slink before release

When you let go, at first, for an instant it keeps its stretch.
You are no longer puling it up.
Gravity is still pulling it down
The stretch of the slinky is pulling it down. Therefore it accelerates down faster than the acceleration of gravity.

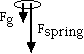
The forces on the top slink after release.

Consider the bottom slink of the slinky.
Gravity is pulling it down. The stretched spring above is pulling it up with a force equal and opposite to gravity.

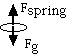
The forces on the bottom slink before and after release.

When you let go, at first the upward force remains the same and so the slink remains in place. As the spring collapses together the upward force descreases and the lowest slink begins to accelerate toward the ground.

The center of mass of the slinky is not at the center because the top slinks are stretched far apart while the bttom ones are closer together.

A Physics Puzzler

We've used force diagrams to explain the fall of the top and bottom slinks of the slinky, what about the fall of the center of mass? We know the center of mass falls at the acceleration of gravity, let's look at the forces on the slink located in the center of the compressed slinky at the center of mass.

Here is the force isolation diagram for the middle slink.

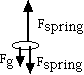
This is the same force diagram immediately before and after the top slink is released. Before release the sum of the forces is zero, the slink at the center of mass is at rest.

So the puzzler is: What's going on here? How can the center of mass accelerate at g if there is no net force on the slink at the center of mass.

Answer below:

The center of mass is not attached to the slink at the center of mass.

The slink at the center of mass indeed does remain stationary when the top slink is released. However, the top of the slink is accelerating down faster than g, so the center of mass of the entire slinky is accelerating down at g.

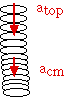
The center of mass can move relative to the slinks.

Etc.

When a bungey jumpers jump off a tower they accelerate faster than g. The stretched elastic of the bungey cord pulls them down in addition to the pull from gravity. So they accelerate down faster than g.

Return to Draft Activities