Making nested mobius bands.
an Article from the Science Column of the Magazine Fantasy and Science Fiction
by Paul Doherty and Pat Murphy, 1998
A Mobius strip is a band of paper that's deceptively simple in its appearance and exceptionally twisted in its properties.
You can make a Mobius strip easily. Just take an ordinary strip of paper, one that's at least 11 inches long and an inch or so wide. Bring the ends of the strip together to make a loop and put a half twist in the loop, so that the top surface of the strip meets the bottom surface of the strip. Tape the ends together.
Voila! You have a Mobius strip&emdash;a devilishly twisted device that can tangle your mind and lead you to peculiar places. Way back in 1858, mathematician August Ferdinand Mobius discovered the peculiar properties of this paper loop. Ever since, topologists (a specially twisted breed of mathematician) have been experimenting and speculating about the properties of this strip and its relatives.
In this column, we'll explore some of the peculiar properties of the Mobius strip, show you some mighty strange new experiments you can do at home, and take a brief excursion into the 4th-dimensional thinking. To come along on this adventure, you'll need some paper, tape, a pencil or pen, a pair of scissors, and a paper clip.
From Simple Beginnings
Start by making a Mobius strip, as described above. To prove to yourself that this piece of paper now has only one side, start at any point on the strip and draw a line, following the length of the strip. Without picking up the point of the pencil, you'll go around the loop twice and end up back where you started. The line will go all around the inside of the loop and all around the outside of the loop&emdash;even though you never picked up the pencil to change sides. That's because the mobius strip only has one side.
Any time you want to test a paper loop to determine whether it's a mobius strip or not, draw a line. Try this with loops with more than a half twist, and you'll find that any loop with an odd number of half twists has one side like a Mobius strip and any loop with an even number of half twists has two sides. Counting, as Paul likes to point out, isn't as easy as your first grade teacher led you to believe. It's difficult to count the number of sides to a piece of paper even though the number is either 1 or 2.
Incidentally, the Mobius strip also has only one edge. You can prove that to yourself by putting your finger on the edge anywhere along the loop. Now run your finger along the edge. Eventually, you end up right back where you started, having gone all the way around the loop twice. Check for yourself that a flat piece of paper has one edge, an untwisted loop made from a paper tape strip has two edges.
Simple dissections
Now think about this: What will you get if you cut your Mobius
strip in half, dividing it down the middle all along its length.
So try it. Maybe you figured you'd get two Mobius strips, but that's
not what happens. You get one long, twisted strip. Check to see if
it's a Mobius strip by drawing a line, and you'll discover it's not.
The new strip has two half twists, so it's not a Mobius strip.
It's this result that prompted some anonymous poet to write the
following limerick:
A mathematician confided
That a Möbius band is one-sided,
And you'll get quite a laugh,
If you cut one in half,
For it stays in one piece when divided.
To twist your mind a little farther, predict what you'll get if you cut this new strip down the middle all along its length. Then try it. This time you get two interlocking rings, each of which has four half twists
Weird, huh? But we're not done yet, though. Make another Mobius strip and try this&emdash;rather than cutting the strip in half, start your cut one third of the strip's width in from the edge, as if you were going to cut a skinny ring off the wide ring. (Of course, you've realized by now that there's no way you're going to do anything that simple.) When you're done, you'll find you have something entirely new: a long loop with two half twists interlocking with a Mobius strip the length of the original. What you've done is cut around the loop twice, cutting near the edge. And since a Mobius strip only has one edge, you have to go around twice to cut that edge off. Basically, you've cut off a strip near the edge, leaving a skinnier version of the original Mobius strip intact.
By the way, there is nothing special about a third. You get the same result if you cut anywhere except the middle of the strip. When you cut the middle of the strip, you meet up with your original cut on your first time around the strip. With any other fraction, you cut off the edge of the strip.
We recommend that you try this dissection technique on paper loops that have various numbers of twists in them. Paul suggests that you use the scientific method--predict what will happen, then test your hypothesis by trying the experiment. Pat prefers to simply whack away with scissors and be amazed by the results. She warns that attempting to predict the results may make your head explode, particularly when you cut a loop with three half twists in it. (Definitely try that one. The results will amaze you.)
Choose whichever approach suits you best. If you chose to adopt the scientific method, that's fine&emdash;this is, after all, a magazine of fantasy and SCIENCE fiction. But some of the properties of a Mobius strip seem more like magic than math, so if you'd rather emphasize that this is a magazine of FANTASY and science fiction, that's all right too.
Counting the twists
While you are doing all this, you may need to count the number of twists in a band before or after you cut it. When you have multiple twists, this isn't always easy.
Here's how we do it. Hold the band so that one surface is flat against a table top and all the twists are on top. Clip a paper clip to the band at a point near you. Run the paperclip along the mobius band counting its revolutions.
If there's just one half twist in the loop and you start out with the head of the paperclip (the part you'd pull on to unclip it) facing to the right, it will end up facing to the left, having gone through half a revolution. To bring it back to its original position, you need to push it around the loop twice.
Double the Weirdness; Double the Fun
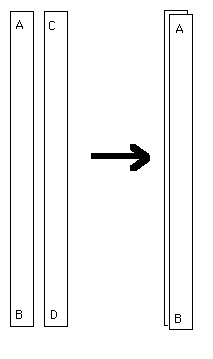
All of that's kind of weird, but we're just getting started. Make two identical strips of paper and label the ends with letters as shown in the picture. Lay one strip on top of the other with end A on top of end C.

Take this double strip and bring the ends together to make a loop. Suppose you taped the ends of the strips together, attaching the A to B and C to D. You'd get two nested loops, right. Simple.
Don't tape them yet. Instead, put a half twist in the loop and bring A to D and B to C. Now tape the ends together so that you have a double layer mobius strip.
Test this double loop and make sure it's a mobius strip. Put your pen at junction A/D and draw a line that runs the length of the strip. You'll come around to junction C/B. Keep going and you'll end up back at A/D. Sure enough, you've gone all the way around the inside and outside of the loop. A one-sided strip, sure enough.
The space between these two pieces of paper is pretty clearly a
mobius strip-shaped space. You can do a little experimenting with
this space using your paperclip. Hold onto one end of the paper clip
and stick the clip between the two strips. Now run the paperclip all
the way around the loop, following the space between the strips. You
can manage this easily enough. The paperclip has just followed a
mobius strip, encountering no obstacles along the way. It seems
obvious that you must have two mobius strips here.
Here comes the surprise. (You know there had to be one.) Try to
separate the two Mobius strips. Surprise! It isn't two Mobius strips
at all. It's one big loop with two full half twists. Once you
un-nest the strips, it isn't a Mobius strip at all.
How strange. It appeared that you had a mobius strip. Now you don't. Paul thinks of the doubly twisted loop that you get when you un-nest the strips as the paint on a mobius strip! That is exactly what it is. This doubly twisted loop formed the surface around a mobius space. And, interestingly enough, the surface around a mobius strip has two sides: the side that's up against the strip and the other side, the outside. We know this because the line that we drew on the single side of the mobius strip is still on the doubly twisted mobius paint strip. That line is on one side of the strip, all the way around it.
With an effort, you can make that big loop back into the nested mobius loop. Give it a try. When you're attempting this, it helps to pay attention to the line you drew on the original, nested, mobius strip. That line will end up on the outside of the strip when you re-nest it.
By the way, the mathematicians mobius strip like the mathematicians plane has no thickness. Some people have trouble remembering this when they deal with mobius strips made of paper, but they can visualize the the mobius strip made of the empty space between the two bands getting thinner and thinner without limit.
Triple the Weirdness...
Intrigued by all this, we took our experiment one step farther
(This is, of course, in keeping with one of Pat's Rules for Living,
"Anything worth doing is worth overdoing.") So we took three strips
of paper, labeled the ends as shown, and stacked them with strip A/B
on top of C/D on top of E/F.
Then we made them into a loop with a half twist, and taped A to F and
B to E and C to D. What do you think we got when we un-nested the
strips?
Oh, come on&emdash;don't give up now. Before, we had the paint on a mobuis strip. Now we've filled in the mobius space with a mobius strip, so we have the paint on the mobius strip. And we have a mobius strip itself, linked to the paint.
The true experimentalists among you have probably already leapt ahead to a few more experiments with this peculiar artifact. Suppose you make a double nested mobius strip as described in B. Then you cut it down the middle as described in A. What would you get? Suppose you cut it 1/3 of the way in? What then? Makes your head hurt, doesn't it? Have a good time!
Implications of twisted thinking
By now, the floor around you is probably littered with twisted paper rings and you're wondering what all this has to do with science fiction. Well, the field is rich with stories that take the Mobius strip one step farther.
In "A Subway called Mobius," A.J. Deutsch postulates a Boston
subway system that becomes more and more complicated until
trains find their way into the 4th dimension. Martin Gardner's
"No-Sided Professor" is about a mathematician who invents a folding
that goes one step beyond mobius and creates a no-sided object. (Paul
likes this one particularly well because it illustrates his rule
about mathematics challenges. He says that when soemone challenges
you to find how few steps you can use to accomplish some puzzle
task--like weighing coins, cutting gold chains, transporting goats,
lions, and cabbage across rivers in rowboats, the answer is always
at least one less than whatever answer you can find. So as
soon as Mobius discovered the one sided strip, Paul figures the
search was on for the no sided strip.)
Science fiction writers are always looking for a way into the fourth
dimension; it's part of our job description. And the Mobius strip
offers some interesting possibilities to those who want to think
about other dimensions.
The Mobius strip has only one side, right? You've proven that by drawing a pencil line all the way around the strip, inside (so to speak) and outside (so to speak), without ever lifting your pencil to go over an edge.
Now suppose you take a hole punch and make a hole through the strip. You might think that hole goes from one side of the strip to the other--but the strip only has one side. So where does the hole go from and to?
It goes from one location on the one-sided strip to another location on the one-sided strip. If you were a two-dimensional Flatlander, this hole could provide startling short cut to a distant location (a spot that the Flatlander would ordinarily have to trudge a long way to reach). That short cut goes through the third dimension, something that a Flatlander living on the strip might have a tough time visualizing.
So if you can give a two-dimensional creature a short cut through the third dimension, then surely we can find a way to provide three dimensional creatures with a short cut through the fourth dimension. For that, science fiction writers consult the theorectical physicists, who are often kindred spirits.
Wormholes and Exotic Matter
For this, we consulted an excellent book by Kip Thorne: Black Holes and Time Warps&emdash;Einstein's Outrageous Legacy. In the final chapter, Thorne describes his efforts to assist Carl Sagan in coming up with a plausible solution for Sagan's novel, Contact. Sagan needed a method by which a character could travel for an hour or so and make her way from near Earth to a position near the star Vega, some 26 light years away. To assist Sagan, Thorne explored the science fictional possibilities of the wormhole, a hypothetical shortcut for travel between distant points in the Universe. Like the hole in the Mobius strip, a wormhole connects two points by taking a shortcut through another dimension.
According to Thorne, wormholes were discovered mathematically way back in 1916, as a solution to Einstein's field equation. But those mathematical wormholes aren't much use for interstellar travel: they appear, connect two points, then pinch off and disappear very very quickly. Thorne writes of such a wormhole, "...its total lifespan from creation to pinchoff is so short that nothing whatsoever (no person, no radiation, no signal of any sort) can travel through it, from one mouth to another. Anything that tries will get caught and destroyed in the pinch-off."
Thorne postulates something called "exotic matter" that holds the wormhole open by pushing its walls apart gravitationally. He discusses the properties of exotic matter at length and indicates that such stuff does indeed theorectically exist: Stephen Hawking's discoveries related to black holes suggest that such matter may exist near a black hole's event horizon. Thorne suggests that, given what physicists know now, wormholes could theorectically be created by an infinitely advanced civilization and held open with exotic matter. He goes on to talk at length about the possible uses of those wormholes.
In the end, it makes the two of us think about that hole through the Mobius strip. A Flatlander mathematician or theorectical physicist might theorize that such a thing was possible, and be accused of indulging in science fiction. From the point of view of the Flatlander, that hole was punched by some unimaginable entity existing in another dimension. From our point of view as three-dimensional creatures, wormholes are similar.
A Few More Paper Dolls
That concludes our excursion into the highly theorectical and intriguing world of theorectical physics. Pat will be continuing her exploration by assisting her friend Max Merriwell in the creation of a space opera. (For more on that, visit Pat's web site at www.exo.net/jaxxx/)
But for those of us who prefer to remain on this planet, here's one more mind-tangling experiment involving paper and scissors and tape. First, cut out a large plus sign, like this
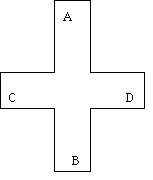
Tape A to B to make a loop, then tape C to D to make a loop but do not connect AB to CD. Now look at this construction carefully and figure out what will happen if you cut either of these loops in half, dividing it down the middle all along its length. When you think you've got it, try the experiment and see if you were right.
After you've done that, predict what will happen if you bisect the other loop in the same way. Then try the experiment. If you manage to predict the result correctly, congratulations on your geometric imagination!
|
Scientific Explorations with Paul Doherty |
|
20 October 2000 |