Introduction

Cutting a Mobius strip and its relatives provides an opportunity to visualize what will happen, make hypotheses, and to be surprised by the results of an experiment.

Material

• Several strips of paper ( a good size is 2.5 cm wide and 25 cm long)
  • if you use brown packing tape with adhesive on one side you can skip the tape below.
• tape
• scissors
• a felt tip pen
• a paper clip

You'll need to master the techniques for counting sides of a loop of paper by drawing a line around its center, and for counting half-twists using a paper clip that were described in the Mobius exploration before you begin this one.

To Do and Notice/ What's Going On?

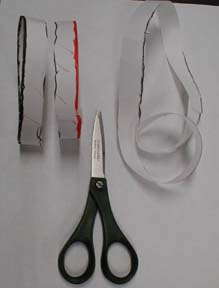
Bend a paper strip into a loop with no twists. Make a line down the middle of your loop.
Visualize what you will get when you cut this loop along the line.

Cut the loop and observe what happens.

Congratulations.

Getting twisted.

Give the paper a half twist and tape or glue the ends together to make a Mobius strip.

Mark a line down the center of this strip.

Visualize what you will get when you cut the Mobius strip along the line.

Perhaps you thought that you would get two Mobius strips. Surprise!

What you get is described in this limerick:

A mathematician confided
That a Mobius band is one-sided,
And you'll get quite a laugh,
If you cut one in half,
For it stays in one piece when divided.

A hoop and a Mobius strip cut in half.

How many sides does the resulting band have? Draw a line to find out.

How many half-twists. Count them with the twist test to find out.

Half a Mobius strip. marked down the middle and taped down for counting twists.

Now cut the resulting band in half.
Another surprise.
Count the number of sides each of the resulting bands possesses.

A half a Mobius strip cut in half again.

Next cut a new Mobius strip one-third of the way in from one edge. The cut will meet itself eventually.

You end up with two loops, you've cut the edge off the original Mobius strip leaving a thinner version of itself intact at the center, and producing a second loop, twice as long, with two half-twists.
Count the sides of, and twists in, the resulting rings.

Try cutting a slice off the Mobius strip 1/4 or 1/5 or some other distance in from the edge. Predict what you expect to happen then do the experiment.

Try slicing strips with 3 half-twists or other numbers of half twists. Predict the answer you expect then do the experiment.

Can you find the rule that tells you how many twists you get when you bisect a loop with n half twists? Hint, Loops with even numbers of half-twists follow a rule that is different from those with odd numbers of half-twists.

What's Going On?

When you cut the Mobius strip in half you made a strip twice as long with 4 half twists.

Cut the half-Mobius in half again and you get two linked strips, both with 4 half twists.

Cut the Mobius strip in thirds and you make two linked loops one with one half twist and one with 4 half twists.

Mark a line 1/n from one side of a Mobius band of width W, then cut along this line.

There will be a strip left in the middle of width W - W/n-W/n.
A strip will be left in the middle for any value of n except n=2.

This is why marking a line down the middle of the Mobius strip, 1/2 way from one edge, produces a different result from all other fractions.

The rule

If you bisect a strip with an even number, n, of half twists you get two loops each with n half-twists. So a loop with 2 half-twists splits into two loops each with 2 half-twists.

If n is odd, you get one loop with 2n + 2 half-twists. So a Mobius strip with 1 half-twist becomes a loop with 2+2 = 4 half-twists.

Scientific Explorations with Paul Doherty

© 2000

20 October 2000