
A lead fishing weight is a great mass.
The meter long string is marked at 10 cm intervals measured from the center of the weight.
"It don't mean a thing if it ain't got that swing."
Pendulums provide an excellent training ground for measurement.

Material
Assembly
Tie the weight onto the end of the string.
Measuring from the center of the weight mark off 10 cm lengths along the string.
To Do and Notice
Hold the string at the one meter mark and start it swinging.
What do you see?
What's Going On?
When you pull the pendulum to the side gravity pulls it back toward the center.
You can feel this force as you pull the pendulum to the side.
The pendulum moves fastest at the bottom of its swing and slower at the ends, in fact it stops and reverses its direction at the ends of its swings. At the bottom of its swing there is no force on the pendulum causing it to continue or to stop its swing, the inertia of its motion carries it through the bottom and up the other side.
Longer pendulums take longer to complete one cycle of swing.
The energy of motion, kinetic energy is maximum at the bottom of the swing and zero at the ends of the swing. The potential energy from gravity is greatest at the ends of the swing and least at the bottom. The energy in a pendulum goes back and forth between kinetic and potential.
Math Root
Measure the period of the pendulum, T, in seconds.
It should be about 2 seconds.
Notes on measuring period.
Start the stopwatch as the weight crosses through the bottom of its swing, stop it also at the bottom of its swing after it has gone through one oscillation.
If you have a group of people doing the measurements have them each post their results, notice the variations. Lead a discussion about what might cause the variations. (Things like human reaction time, not measuring a full period etc.)
You can make make accurate measurements by timing ten swings of the pendulum. Divide the period for 10 swings by 10 to find the period of one swing.
How to measure the time for ten swings.
To measure the period of ten swings start the stopwatch as the pendulum swings through the bottom of its arc and count "zero" It is really important to start with zero otherwise you will get the wrong period. Then each time it crosses through the bottom going in the same direction count, one,two,...nine, then stop the watch at the count of ten.
Make a Table
Make a table and measure the period as a function of length, L.
Notice that the period increases as the length increases.
Examine your table.
Compare the periods for a half meter long pendulum and a one meter long pendulum. How does the period change when you double the length of the pendulum. The period of the half-meter pendulum is 1.4 seconds while the period of the meter pendulum is 2 seconds. When you double the length the period increases times 1.4.
Notice that 1.4 is just about the square root of 2.
Make a graph of period versus length
Examine your graph.
Does it look like the graph of the square root?
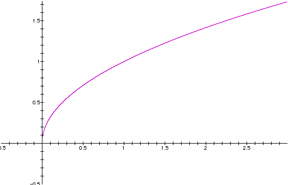
Make a new Graph
To see if it is really a square root, plot the period versus the square root of the length.
If the period really is proportional to the square root of the length, the data will lie on a straight line.
Optional Graph
Plot the base 10 logarithm of the period in seconds, log T, versus the log of the length in meters, log L.
If the period is proportional to the square root of the length the data will lie on a straight line of slope 1/2.
The period of a pendulum is proportional to the square root of its length.
In fact the period, T, in seconds is predicted to be
T = 2p (L/g)0.5
Where L is the length of the pendulum in meters and
g is the acceleration of gravity, 9.8 m/s2
Where does the 2p come from? Answer.
Going Further
Investigate how the period of a pendulum depends on the mass you hang at the bottom.
Investigate how the period of the pendulum depends on the amplitude of the pendulum, i.e. how far you pull it to the side.(To do this you might want to use a protractor to measure the amplitude in degrees.)
We found that:
The period does not depend much on the mass hung at the bottom as long as the mass is much heavier than the string.
The period does not depend much on the amplitude, unless the amplitude starts getting much bigger than 10 degrees.
Etc.
A pendulum with a period of 2 seconds is called a "seconds pendulum." The length of a pendulum with a period of 2 seconds was originally proposed as a way to define the meter. This definition was not accepted however, instead, the meter was defined as a ten millionth of the distance from the earth's equator to the pole on a line of longitude through Paris.
Advanced Math Root
For a pendulum of length L and mass m, the component of the force of gravity pulling the pendulum back toward the center of its swing is
Fc = -mg sin q
The minus sign means that when we pull the mass away from the center gravity pulls it back toward the center.
Where mg is the mass of the pendulum times the acceleration of gravity, this is the total gravitational force also known as the weight.
q is the angle measured from the bottom of the swing, when the pendulum is at the bottom of its swing q = 0.
If we write Newton's law
F = ma where a is acceleration = d2x/dt2
then substitute we get
d2x/dt2 = F/m = g sin q
When the angle, q, is measure in radians and the angle is small, less than 0.1 rad then we can make the approximation that sin q = q.
Now the angle q is approximately x/L
So,
d2x/dt2 = -g x/L
This differential equation has the well known solution
x = A cos wt
where w = (g/L)0.5
This is a sinusoidal oscillation with amplitude A and period T = 2p/w = 2p (L/g)0.5
Now you can see where the 2p comes from. There are 2p radians in a circle and the sinewave completes one circle when 2p = wt or when t = 2p /w.

References
Physics 3rd ed., Paul A. Tipler, Worth Publishers, p 382-384 Pendulums, uses calculus.
|
Scientific Explorations with Paul Doherty |
|
26 Sep 2000 |