Particle Accelerator
Small pushes delivered at just the right time can
accelerate a coin rolling in a balloon to high speeds. In addition,
as friction removes energy from the coin, it circles closer to the
bottom of the balloon and slows down.
Material
- A spherical balloon 9 inches (25 cm) or more
in diameter when inflated. Clearer balloons are
better.
- A coin e.g. a quarter( optional, two
coins.)
Assembly
Put the coin into the balloon.
Inflate the balloon.
Tie off the neck of the balloon.
To Do and Notice
Move the balloon in a horizontal circle.
Try to get the coin to roll in a circle around the inside of the
balloon.
Notice that you can feel the coin as it passes
over your hand.
Try to get the coin to go faster.
Notice that if you move your hands in a circle at just the right rate
you can accelerate the coin to high speed.
As the coin speeds up it rolls higher in the
balloon. At the highest speeds it orbits around inside the balloon at
the equator.
Stop adding energy to the balloon. Notice that as
the coin loses energy it moves more slowly and orbits closer to the
bottom of the balloon.
What's Going On?
The coin rolls on its edge inside the bottom
hemisphere of the balloon.
To stay in its orbit and not roll down the
inclined plane to the bottom of the balloon an upward contact force
from the balloon is needed. This contact force is the result of the
motion of the coin in its circular orbit. The balloon must exert an
inward centripetal force on the coin to accelerate it into its
circular motion, at the same time the balloon exerts a vertical force
on the coin.
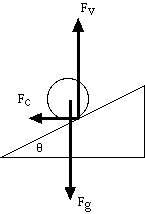
A ball rolling on an inclined plane: Gravity, Fg,
pulls down, the contact force of the plane on the ball is resolved
into two parts, a horizontal force, Fc, which provides the
centripetal force and a vertical force, Fv. I have assumed
there is no friction force so that the total contact force is
perpendicular to the plane.
Math Root
A coin can be at rest on a horizontal surface.
However, as the angle of the inclined plane that the coin is rolling
along increases, the upward force exerted by the inclined plane on
the coin must increase to keep it from sliding down.
This upward force is the vertical part of the
contact force of the inclined-plane wall of the balloon on the coin.
If the coin is rolling along a banked curve, like the inside of a
balloon, the horizontal component of the contact force must supply
the centripetal force necessary to keep the coin moving in a
circle.
The centripetal force to keep a coin of mass m
moving at velocity v in a circle of radius r the required force
is:
Fc = m v2/r
The vertical force necessary to keep a coin of
mass m at rest while rolling along an inclined plane which rises at
an angle q
with respect to the horizontal is:
Fv = mg
Where g is the acceleration of gravity.
These forces are related by the requirement that
their sum is perpendicular to the plane
Fc/Fv = tan q
so mv2/r = mg tan
q
v2 = rg tan
q
So that at lower angles the velocity is slower at
higher angles the velocity is greater.
The balloon has lower angles near the bottom (and
smaller radius too) so the velocity is slowest near the
bottom.
So What?
A particle accelerator such as a cyclotron or a
synchrotron pumps energy into an orbiting particle as it orbits
inside the accelerator. The coin inside the balloon models the action
of an accelerator.
Going Further
Optional Put two coins into a balloon, notice that
if you start them orbiting in the same direction, they eventually
roll around together.
Optional With two coins in the balloon it is
possible to get the coins to orbit in opposite directions and to pump
energy into both coins at the same time.
Get the coin orbiting inside the balloon. Then
throw the balloon into the air. Notice that the balloon wobbles. A
distant star wobbles when a planet orbits the star. From the wobble
of the balloon we can tell there is a coin inside it, even if we
cannot see the coin. The wobble of the star reveals the presence of
an invisible planet.
Return to Draft
Activities
