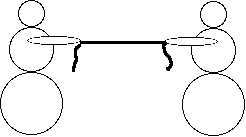
Two people pull on a string.
Get it together.
Material
To Do and Notice
Have two people set up a tug of war.

Each person notes that the string is exerting a force which is pulling them.
What are the forces on the right side person?
What are the forces on the string?
You can put a bathroom scale under the people to measure the forces that the floor exerts on them, you can use a spring scale meant to weigh fish to measure the force that the string exerts on them.
What's Going On?
To use Newton's Laws you start by drawing the situation and then isolate one of the objects in the situation by drawing a boundary around it. Then you drawing all of the forces acting on that object from outside through the boundary, and ignore all of the forces which only act inside the boundary.
The forces on the person
So for the right hand person there are 4 forces.
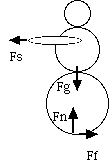
The gravity force is equal and opposite to the normal force which the floor exerts on the person. The friction force from the floor is equal and opposite the force from the string.
The net force on the person, the sum of the forces is zero.
So how can anyone win a tug of war?
Well, if the force from the string becomes larger that the force of friction the sum of the forces is no longer zero and so the person accelerates to the left.
(You may notice that even though the pairs of forces are equal and opposite they are not along the same line. The pairs of forces thus exert twisting forces or torques on the person. The two torques are equal and opposite and sum to zero.)
Now consider the net force on the string.
The forces on the string are also equal and
opposite, and also along the same line.
I have ignored the gravity forces on the low mass string.
So the net force on the string is zero and the string does not accelerate.
If one person exerts a larger force on the string than the other person then the string will accelerate. (Since the string is very light compared to the mass of the persons, the difference in the forces on the string remains small.)
Action-Reaction
Newton said that the action is always equal and opposite to the reaction.
Thus in a problem like the one above their are pairs of forces which are action and reaction pairs.
Which pairs are action reaction pairs.
Here's a hint. The two forces in an action-reaction pair each act on a different object.
One action reaction pair is the force of the person on the floor and the force of the floor on the person.
Another is the force of gravity of the earth on the person and the force of gravity of the person on the earth.
Another is the force of the string on the person and the force of the person on the string. These forces are always exactly equal and opposite.
So on the person, gravity and the normal force are not an action-reaction pair even though they are equal and opposite they are one the same object.
Also the forces on the string Fsl and Fsr are not an action reaction pair, why?
Note that these forces can sometimes be unequal.
|
Scientific Explorations with Paul Doherty |
|
4 October 2001 |