Introduction

At most places on earth, where the ocean meets the land, there are two high tides each day. In this series of activities we'll explore why there are two tides per day, why the tides occur 54 minutes later each day, and why the heights of the tides change over the course of each month.

We'll use several activities to investigate and model the tides.

1. Why are there two high tides per day?
2. The Dance of the Tides., modeling tide creating forces by dancing.
3. Why does the high tide arrive later each day?
4. Why do the tides change height during a month?

Introduction

The moon produces two tidal bulges on the earth on a line connecting the centers of the earth and moon.
The earth rotates once a day.
Therefore every place on the equator of the earth moves under the two high tides per day.

Material

A piece of corrugated cardboard at least 20 cm x 20 cm square.
A pushpin or thumbtack.

Assembly

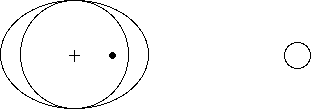
Copy the Earth-moon system drawn below onto heavy paper and cut it out.
(Leave the moon connected to the earth by some paper.)

Push a thumbtack through the Barycenter (the center of mass = •) of the Earth-moon system into the center of the cardboard.

The earth and moon viewed from above the north pole. Tides and the center of mass, • , are shown.

To Do and Notice

Swing the moon around the earth in its monthly orbit, pivoting it around the tack through the center of mass. (It takes 27.3 days for the moon to orbit the earth once with respect to the fixed stars.)

Notice that as the moon goes around the center of mass so does the center of the earth.

What's going on?

There tide raising force,is due to the decrease in the force of gravity with distance. For a spherical object the gravity force falls off as the inverse square of the distance.

The gravitational contribution can be isolated by doing a thought experiment: stop the orbital motion and allow the earth and moon to free-fall together.

Bits of mass on the earth nearest the moon experience the largest force, masses farthest from the moon experience the least force and of course masses near the center of gravity of the earth experience a force that is "in the middle"(This is often referred to as a Goldilocks problem.) If these masses were not pulled together by the gravity of the remainder of the earth they would fall toward the moon at different accelerations. The nearest one would accelerate faster and leave the middle one behind, the farthest one would accelerate slowly and be left behind by other faster-accelerating masses.

Points on the earth nearest the moon experience larger accelerations than those furthest from the moon, this contributes to the formation of two tidal bulges on earth one nearest the moon and one on the other side.

Now consider a body in free fall experiencing orbital motion.

Consider a small spacecraft orbiting the earth, there is just one speed that will allow it to orbit the earth in a circle of a given radius.
Higher speeds are needed for orbits closer to the center of the earth.
Slower speeds are needed for more distant orbits.

Before we continue we must separate the rotation of the earth about its axis which causes the equatorial bulge from the motion of the earth in its orbit around the barycenter, called its revolution.

If the earth did not rotate then as it went around in its orbit of the barycenter every point on the earth would go around in the same circle in the same time.

The center of mass of the earth orbits the center of mass of the earth-moon system, held into its orbit by the gravitational pull of the moon.

Points near the center of gravity of the earth, orbit the moon so that the lunar gravitational force on the whole earth provides the exact acceleration needed to keep them in their circular orbit, they are in orbital freefall.

Points farthest from the moon are swung around in the same circle in the same month of time,and so need the same force as that on the center of the earth to hold them in orbit, and yet, they are farther from the moon so that the lunar gravity is weaker. To hold the earth together there must be an additional force to keep them in their orbit. This additional force comes from the gravitational atraction of the earth itself and results in the stretching of the distance from the center of the earth to the surface, creating a tidal bulge on te opposite side of the earth from the moon.

Points nearer the moon than the center of the earth orbit in thr same circle, yet the force from the moon is greater, So another force is necessary to reduce the force of attraction of the moon to create the correct circular motion. This force comes from the gravitational pull of the earth after the surface bulges toward the moon. Thus there is a tidal bulge toward the moon o the side of the earth nearest the moon.

To Do and Notice

You can model the gravitational contribution to the tides with the following dance.

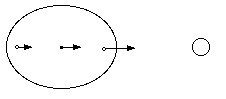
Arrange three people in a straight line one pace apart. (A pace is the length of one relaxed step, about a half-meter.) Place another lone person 8 paces away on the same line. The lone person is the moon.

Have the person nearest the moon take 3 paces toward the moon, the person in the center take 2 paces and the person furthest away take 1 pace. These people are modeling the distance that a mass would fall under different accelerations.

Notice that the people have moved apart.

What's Going On?

This is what would happen to masses located on the earth if they fell toward the moon and weren't held together by their own gravity. In reality, the gravity forces between these masses and the others that make up the earth act like springs holding them together. As the earth falls around the moon in its orbit, these springs are stretched by leading to the tidal bulges.

The point nearest the moon bulges out toward the moon and the point furthest from the moon is left behind.

This leads to two tidal bulges.

The earth rotates under these two bulges once each day and so there are two tidal bulges a day.

The tides arrive later each day by 54 minutes.

Introduction

The earth rotates on its axis as it revolves around the center of mass of the earth moon system.

Assembly

Cut out this earth globe.

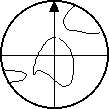
Remove the thumbtack from the barycenter of the first model.

Push the thumbtack through the center of the earth globe then through the earth moon tide model.

Rotate the earth counterclockwise while looking at the lunar tides.

Notice how any spot on the surface of the earth rotates under two high tides each day.

Set the earth so that the Greenwich meridian, indicated by the arrow, points toward the moon. In our simple model the tide at Greenwich is high.

Rotate the earth through one full solar day, so that the Greenwich meridian goes around in one full circle.

While the earth is turning the moon moves in its orbit. In one day the moon moves 13 degrees counterclockwise ( degrees per day = 360 degrees/27.3 days). To arrive at the high tide again, the Greenwich meridian has to catch up with the moon. This requires 54 minutes. (approximately 24 hours *13/360)

What's Going On?

Thus, the high tide gets 54 minutes later each day.

The height of the high tide changes over the course of the month.
It is highest at new moon and full moon and lowest at first and third quarters.

Introduction

The sun also pulls up tides, these add to the moon tides and create a pattern of tides which range from high, spring tides, to low, neap tides, twice each month. Since the phases of the moon also depend on the position of the moon and the sun, the tidal pattern follows the phases of the moon.

Assembly

Cut out the solar tide model below.

Push a pin through the earth globe, which will be on top, The solar tide model in the middle, and on the bottom the lunar tide model which includes the moon, into some cardboard.

Optional: If you have access to a transparency maker, make a transparency of the lunar tide model. Glue the solar tide model to some heavy cardboard, Push a thumbtack through the center of the earth model then through the center of the earth in the transparency of the lunar tide and finally into the center of the solar tide. This will allow you to see the smaller solar tide through the transparent, larger, moon tide.

To Do and Notice

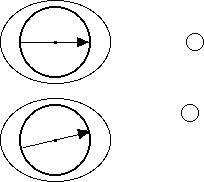
Align the high tides pulled up by the moon and the sun and notice that the tides pulled up by the sun are about half as high as the tides pulled up by the moon.

When the moon is directly between the sun and the earth it is a new moon and the tides are aligned and add. This causes the highest tides called spring tides (spring as in "to leap up" not as in a season.)
(You have to do the addition of the tidal bulges in your head.)

Rotate the moon in its orbit counterclockwise by 90 degrees. Do not allow the sun tides to move. The moon is in its first quarter. Notice that the high tides produced by the sun fill-in the low tides produced by the moon. This combination of tides has the smallest change from high to low are called neap tides.

Move the moon to the opposite side of the earth from the sun, full moon.
Notice that the tides add again.

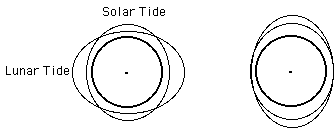
Lunar and solar tides at right angles and aligned

What's Going On?

The force of the sun on you as you stand on the surface of the earth is 180 times greater than the force of the moon on you. But it is not this force that raises the tides but the difference in the gravitational force from one side of the earth to the other. While the force from the sun is greater, the sun is also much more distant, so that the change in the force of the sun across the earth is smaller, a mere 0.017 percent, than the change in the lunar force, 6.7 percent. As a result, the solar tide is smaller than the lunar tide. (In fact .017% * 180 = 3.06 so solar tidal affects are about half of lunar ones.)

It’s more complicated than that.

The simple models presented above can help you understand the mechanics of the tides, but real tides in the earth's oceans are more complicated. For example, the high tide arrives in Santa Cruz two hours earlier than it arrives at the Golden Gate Bridge, a mere 60 miles north, even though the moon is over both places at the same time. The delay is caused because water is a fluid and moves from place to place. As the water flows it experiences drag against the continental shelves, and is pushed to the side by coriolis forces from the spinning earth. The result is that the tidal bulges in the ocean do not line up with the moon.

Solid earth tides

The “solid” earth behaves like a liquid rising and falling in response to tidal forces. The tides in the solid earth were discovered in the sewers of Chicago at the turn of the century. Chicago had installed a new crosstown sewer, and engineers had done their best to get it level, yet twice a day the water height in the sewer varied. The change in the water level in the sewer was due to the motion of the surface of the earth in response to tidal forces from the moon and the sun. The high earth tide occurs pretty close to but not directly underneath the moon, (it lags behind the moon by a mere 4 degrees.)

The tides in the oceans do not line up with the moon.

The oceans are resonant oscillators with periods of tens of hours (depending on the Ocean). They are driven by tidal forces with a period of twelve hours. Whenever you drive a system near its resonant frequency you will find phase shifts between the driving force and the resulting motion. This is why the motion of the water of the oceans does not produce high tides when the moon is overhead. The gravity of the moon does create the tides. The exact time of the high tide depends on where you are along the edge of the Ocean.

There are places with large resonant tides such as the Bay of Fundy where tidal changes can be as high as 40 feet! There are also nodal points in the ocean where there are no tides, these no-tide places are called amphidromic points.

Tides at Hopewell Rocks on the Bay of Fundy come in across miles of mudflats and rise to the tops of the arches. Signs warn visitors to return to the tops of the cliffs before high tide arrives.

The Rotation of the Earth is slowed by Tides

There are fossil corals called "horn corals" that have daily, monthly, and yearly growth rings (Recall trees which have yearly growth rings.) These corals record that there were 400 days per year a three hundred million years ago. This is because the earth used to rotate faster so that the length of one day was shorter, the length of the year remains about the same.

Today we use atomic clocks to measure the slowing down of the earth by tidal drag. In most years we have to add a "leap-second" to adjust for the slowing down of the rotation of the earth.

References:

Exploring Oceans Magazine, The Dance of the Tides, by Paul Doherty, Published by the Exploratorium Winter 1995, Vol 19 #4.

Physical Oceanography, Project Earth Science , Brent A. Ford and P. Sean Smith, Published by the NSTA 1995, pp 141-145. "he Bulge on the Other Side of the Earth."

Return to Draft Activities

Scientific Explorations with Paul Doherty

© 2003

rev. 6 March 2012