Everything in the universe, almost
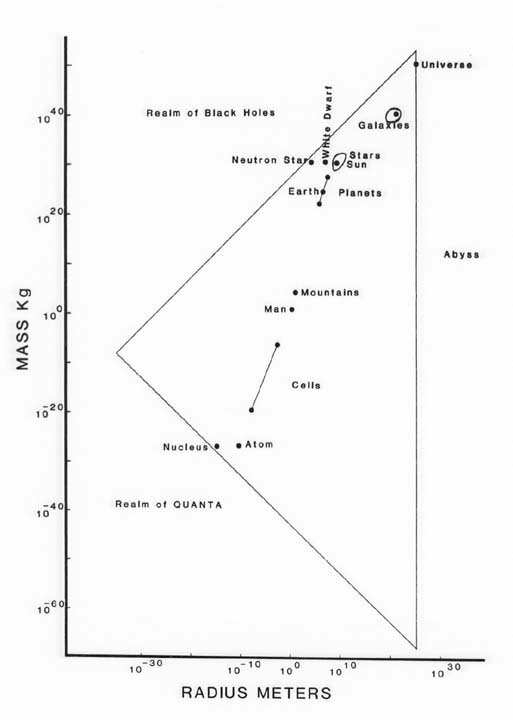
Mass plotted versus radius on a log-log plot including almost
everything known to science.
Click to enlarge.
Everything in the universe, almost

Mass plotted versus radius on a log-log plot including almost
everything known to science.
Click to enlarge.
Introduction
To comprehend the span of sizes of things in the Universe known to science it helps to collect data on the radii and masses of objects and then plot these on a graph.
Material
Graph paper with a centimeter grid.
(Available in the book Graph Paper from your
Copier.
and online through several sources one of which is http://mathpc04.plymouth.edu/gpaper.html )
Assembly
Gather information on the radius and mass of each
of many different objects in the universe.
Look up the values or make estimates.
To simplify comparisons convert all radii into meters and all masses into kilograms.
The goal is to find the radius and mass to within
an order of magnitude.
Since we are only interested in the answer to within a power of 10 we
can ignore details, for example people are usually longer than they
are wide. Yet, we can still say people have a radius of about 1 m.
This is correct to within an order of magnitude since there are no
adult people with a dimension as small as 10 cm or as large as 10
m.
If the object you wish to measure comes in a range of sizes, choose
the radius and mass of a typical or famous object first, then try to
find the largest and smallest of these objects.
The mass of a man might range from a little over 1 kg for a premature
baby to much less than 1000 kg for a large adult. However the average
human will have a mass within an order of magnitude of 100 kg.
To Do and Notice
At first gather data on things you could measure or estimate yourself:
Try to plot the mass on the vertical axis and the radius on the horizontal axis of a graph. You cannot do it. The data spans too much of a range. You need to plot the data on a special type of graph in which each step along the axis is a power of 10.
To fit everything in the known universe onto one graph you will need to include a range of masses from 10-70 kg to 1060 kg and a range of radii from 10-40 m to 1030 m. This means that your vertical axis will span 130 orders of magnitude, and your horizontal axis 70. To do this on an ordinary sheet of graph paper you will need to make 2 cm represent 10 orders of magnitude.
To go beyond what we can measure ourselves into the realm of atoms or of galaxies we extend our senses and our measuring abilities by using instruments: telescopes, radiotelescopes, microscopes and electron microscopes. In these realms it is advantageous to find the measure of a typical specimen and also the range of sizes from the largest to the smallest. For example, find the radius and mass of our sun and then find the smallest and largest known star. Another example would be to find the size of the earth and of the smallest and largest known planet. Looking for these measurements will make you an explorer of the universe, as you look you will stumble over many interesting questions and phenomena, and like Columbus in search of China, while looking for the smallest star you may stumble upon neutron stars, a whole new continent of interesting science.
You might look for:
and at a smaller scale look for:
Notice that when you plot all of these objects almost all of them fall on one line&emdash; a line that ranges from atoms through stars. Few things are far from this line, for example: nuclei, and neutron stars are to the left, while galaxies are to the right.
Let’s add three lines to the graph within which we will find most of the objects known to science.
Line 1, The edge of the known universe
When scientists look out they find that the edge of the visible universe is about 1010 light years away. (Aside, looking out in space is looking back in time so what they see is the big bang which happened 1010 years ago.) So draw one vertical line at a radius of 1026 m. (10^10 years * 3*10^7 s/year * 3*10^8 m/s) We cannot observe anything beyond this line. So, experimental science, which depends upon observation, is limited by this line. Anything beyond this line is difficult to access via experiment. So a question of what lies beyond the edge of the visible universe lies outside of current science.
Line 2 The event horizon of a Black Hole
There is another boundary to experiment in the universe, information cannot cross from inside a black hole to the outside. So, the edge of a black hole, called the event horizon, is a boundary barring experiments.
For any given mass there is a radius at which it becomes a black hole, light or anything else which carries information cannot escape.
The radius of the event horizon of a black hole is
r = GM/c2
where G is the universal gravitational constant, 7
x 10-11 N m2/kg2,
M is the mass of the object in kg,
and c is the speed of light, 3 x 108 m/s.
So the radius of a solar mass black hole is 103 m,
while
the radius of a human mass black hole is 10-25m.
Plot these two points on the graph and connect them by a line. The
event horizons of all black holes are on this line of slope 1. The
slope of one says that the radius of the black hole is linearly
proportional to the mass, i.e. r is proportional to m1. All of experimental physics is
below and to the right of this line. So any discussion of what is
inside a black hole( beyond its mass, charge and spin,) is not
accessible to experimental physics.
Interesting mathematical aside, if you set up the equation for escape velocity in Newtonian mechanics solve it for the radius at which escape velocity is the speed of light then
1/2 m v2 = GMm/r so r = 2GM/c2
You get the equation for the radius of a black hole too large by a factor of 2.
Line 3 Quantum limit
Every particle has a wavelength associated with it called its deBroglie wavelength. The deBroglie wavelength is the wavelength of the quantum mechanical wave describing a particle of mass, m, and speed v. The deBroglie wavelength is inversely proportional to the mass and the velocity of a particle. This means that there is a shortest possible wavelength associated with each particle as it approaches the speed of light. This shortest possible wavelength is called the Compton wavelength and is
r = h/mc
where h is Planck’s constant, 6 x 10-34 J s
m is the mass of the particle in kg
and c is the speed of light, 3 x 108 m/s
The Compton wavelength of a proton is 10-15 m
The Compton wavelength of a person is 10-44 m
These two points can be used to draw a line of slope minus one on the
graph.
The line of Compton wavelengths restricts the questions physicists can ask about a particle, Quantum effects become important at the scale of the Compton wavelength and restrict what experiments can tell us.
What’s Going On?
Only by plotting the power of ten of the radius or mass of an object on the axes of a plot can the entire range of sizes and masses known to scientists can be graphed on one piece of paper.
Most objects lie near one line, these objects are all made of atoms touching each other, objects to the left of the line, e.g. neutron stars, are much denser than atoms, while objects to the right are less dense e.g. galaxies, which encompass mostly vacuum.
Math Root
A graph in which an equal distance along each axis
represents a step of a power of 10 (or some other constant) is called
a log-log plot. Such a plot allows you to graph objects spanning a
huge range of values. In addition, straight lines on a log-log plot
represent power law relationships between the axes y
=
xa . For
example the straight line on the graph of mass, M, versus radius, r,
can be measured to have a slope of 3. This means that there is a
power law relationship between mass and radius, in particular that
mass is proportional to he cube of the radius, M
is proportional to r3. Since we know that mass is
density times volume and volume is radius cubed, such a relationship
implies that everything near this line has about the same density,
the density of water.
(Of course the density of the earth is over 5 times the density of
water while the density of osmium is 20 times that of water but they
are still close to the line representing water.)
Consider a variable y which is a function of a variable x. If you plot the log of y versus the log of x and get a straight line then:
log y = a log x + b
10log y= 10a log x + b
y = 10b xa
or
y = c xa
y is related to x via a power law.
Etc.
In their book Powers of 10 , Philip and Phylis Morrison begin:
The world at arm’s length, roughly one meter in scale, is the world of most artifacts and of the most familiar of living forms. No single building crosses the kilometer scale, no massive architecture, from pyramid to Pentagon, is so large. A similar limit applies to living forms, the giant trees hardly reach 100 m in height, and no animals are or ever have been that large. The smallest individual artifacts we can use and directly appreciate, the elegant letters in some fine manuscript, or the polished eye of a fine needle, perhaps go down to a few tenths of a millimeter. Six orders of magnitude cover the domain of familiarity
The Universe is known to be made of: 4% Atoms, 23% Cold Dark Matter, 73% Dark Energy, In the above MR diagram we only include atoms and their near relatives, nuclei and neutron stars, we do not include dark matter nor do we include dark energy. (This is the result from the WMAP spacecraft.)
MR Diagram
Some Numbers
Object Radius m Wavelength m Mass kg Universe 1026 1051 Galaxy Milky Way 1021 1041 Star Sun 109 1030 planet earth 107 1025 Man 100 102 bacterium virus atom hydrogen 10-10 10-27 electron 10-30
Supermassive Black Hole
1013
1040
Solar Black Hole
103
1030
nucleus hydrogen
10-15
10-27
proton
10-15
10-27
10-13
|
Scientific Explorations with Paul Doherty |
|
8 November 2004 |