There are parts to this activity., in the first part you will build and observe a syphon.

Introduction

We don't often think of water acting as a spring under tension. Yet in a syphon that is what happens.

Material

A glass full of water.

A sink

A piece of clear plastic tubing about 25 cm (10 inches) long, such as Tygon tubing, The tube should be at least 6 mm (1/4 inch) in inside diameter but less that 12 cm in inside diameter (1/2 inch).

To Do and Notice

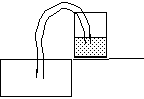
Take a glass half-full of water, place it on the edge of a sink.

Fill the tube with water.

Put the tube completely underwater until it fills with water. Then, cover both ends of the tube with your fingers.

Place one end of the tube into the glass and drop the other into the sink.

Open both ends of the tube.

Notice how the water flows up into the tube, over the rim of the glass and down into the sink.

What's Going On?

Water is cohesive, it sticks together.

If the open end of the tube in the sink is below the water level in the glass water will be pulled down by gravity and flow into the sink. This flowing water will pull the water above it and so on until the level of water in the glass goes below the exit level of the tube or until the level of the water goes below the entrance of the tube.

Etc.

A syphon cannot be more than 10 meters (33 feet) above the water level in the glass.

Consider a chain draped over a low friction pulley.

The tensions between the links of a chain that drapes down equal distances on each side of a pulley.
The net force on every link is zero, there is no acceleration of the chain.

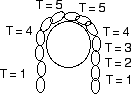
If the chain drapes down equal distances on both sides of the pulley it does not move.

However, if one end of the chain is lower than the other end then gravity will pull down more on the long side of the chain and the chain will accelerate down on the long side.

If one end of the chain hangs down lower than the other the net tension force on the top link does not add to zero and the chain accelerates toward the long side.

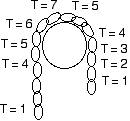
If there is a pile of chain in a glass, and the chain runs up over the pulley, then all of the chain will be pulled out of the glass if the free end hangs below the top of the pile of chain in the glass.

If you dive down into a swimming pool you can feel the pressure of the water on your eardrums increase.

If you put a "playtex living glove" on your hand and then stick your hand into a swimming pool then you will feel the pressure of the water on your hand. (You can also use a plastic bag that the morning paper is delivered in.) The pressure increases with depth.

Now consider a tower full of water sticking up out of the swimming pool. What happens to the pressure as you swim up inside the tower. What happens to your eardrums.

A 10 meter high water tower extends up out of a pool.
There is one atmosphere of pressure at the surface level of the pool.
A bubbles is shown expanding as it rises into the tower.

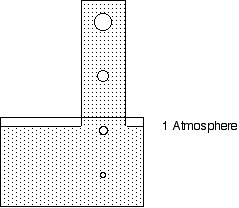
As you go up the pressure decreases.

Questions to ponder.

If you spend time at depth you risk getting the bends. If you spend time in the water tower do you get the straights?

At the top of a 7 m high tower do you risk altitude illness? A 10 m high tower?

Math Root Hydrostatic Pressure

The equation for the pressure, P, in pascals, as a function of depth, h, in meters, below a surface exposed to atmospheric pressure Po is:

P = Po + rgh

where r is the density of water, 10^3 kg/m^3

and where g is the acceleration of gravity, 10 m/s^2

and where Po, atmospheric pressure is approximately 100 kPa or 10^5 Pa.

So at 10 m depth the pressure is P = 10^5 + 10^3 * 10 *10 = 2 * 10^5 pascals , or two atmospheres.

Up in the water filled tower above the swimming pool the depth is negative. So 5 meters up the tower the depth is -5 m and the pressure is

P = 10^5 - 10^3 * 10 * 5 = 5 * 10^4 pascals or one-half an atmosphere.

This is the pressure at 15,000 feet and people 5 meters up the tank had better watch out for altitude illness.

Water Molecules

Water molecules are connected by hydrogen bonds. At one atmosphere of ambient pressure these hydrogen bonds have an equilibrium length.

Picture them like little springs.

When you go deeper underwater the pressure increases above atmospheric pressure. The pressure increases by 1 atmosphere for every 10 m of depth.

Even though water is very incompressible it does compress some. (See the Math Root on water density below) This means that the bonds between water molecules get shorter under higher pressure and get longer under lower pressure.

Math Root Water Density

(The bulk modulus of water, B, is 2 x 10^9 pascals so that water with volume V will change volume by DV under an additional pressure P by DV/V = P/B

One atmosphere is 10^5 pascals so under 1 extra atmosphere of pressure at a depth of 10 meters (30 feet) water decreases its volume by DV/V =10^5/(2*10^9) = 5* 10^-5 or one half of one hundredth of a percent or 50 ppm..)

In the deep ocean 4 km below the surface where the pressure is increased by 400 atmospheres the change in volume of water is DV/V = P/B = (400*10^5)/ 2 x 10^9 = 2 x 10^-2 or two percent.

This means that water in the deep ocean is two percent denser than at the surface. (Ignoring temperature changes.)

The Ball and Spring Model of a Syphon

Picture a syphon tube full of molecules of water all in a row, the molecules are connected by springs.

The molecules go up from one mouth of the tube submerged in water, and over the curved top of the tube down to the exit of the tube.

Start with the tube exit exactly at the level of the water surface in the glass.

This is similar to the chain example.

Water molecules in a syphon connected by hydrogen bond springs.

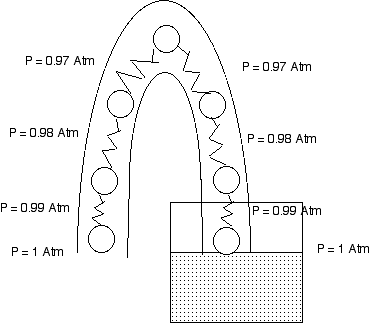
Each spring in the line is longer as we follow the molecules up from the water surface and the open end. When we get to the molecule at the top of the curve the springs on either side are equally stretched and so exert equal and opposite forces on the top molecule. Everything stays at rest.

If we drop the open mouth of the tube down a few molecules and assume the water is at rest we find that the molecule at the top has a spring on the open mouth side that is stretched more than on the water glass side. This causes that molecule to accelerate toward the open mouth side. This stretches the spring on the water glass side of that molecule and pulls along the next molecule in line toward the water glass. This continues until all of the molecules in the tube are in motion.

When the open end of a syphon is below the water level the pressures in the tube result in nonzero net forces which accelerate the water up the tube from the reservoir and out the open end.

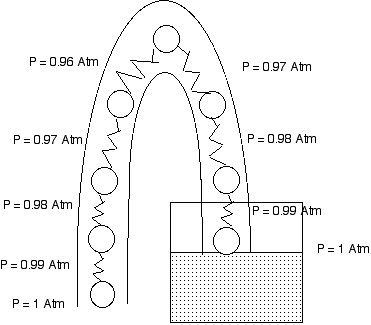
The Pressure Explanation of a Syphon

The pressure at the water surface in the glass is atmospheric pressure.

The pressure at the open mouth of the tube is atmospheric pressure.

Ten centimeters higher in each tube the pressure is 1% lower than atmospheric pressure.

If the open mouth of the tube is at the same level as the water surface, we assume the water is at rest and we find that the pressures on both side of the tube decrease and reach the same value at the top of the tube. The water is indeed at rest.

However if the mouth is lower than the water surface, when we get to the top of the tube the pressure on the open side is less than the pressure at the water side. this means that the water at the top of the tube accelerates toward the mouth of the tube. And so water flows out of the tube over the top.

An awkward problem

When the syphon stretches more than 10 m above the surface of the water then the pressure in the tube goes below zero, it becomes negative.

If there are any air bubbles in the tube the water will rupture and you cannot syphon water over a hill higher than 10 m.

However in a thin tube of perfectly clean water you can pull a column of water up until the pressure has a very large negative value. The hydrogen bonds between the water molecules are really stretched under these conditions and the water is actually under tension.

Scientific Explorations with Paul Doherty

© 2005

5 April 2005