
Two snapshots of a slinky rotating around.
It’s fun to swing
Introduction
A vertical slinky hung from its top with the bottom free can be swung around so that its shape models the resonances of a tube closed at one end and open at the other.
Material
A plastic or metal Slinky
Optional, a stopwatch
To Do and Notice
Hold a slinky by one end and let the other end
hang.
If the bottom of the slinky hits the floor, let only a portion of the
slinky hang down from your hand. Or stand on a ladder.

Move the hand holding the slinky slowly around in
a small circle like you were stirring a pot of soup.
Search for the correct speed so that the bottom of the slinky makes
the largest possible circle.
Notice that the the slinky makes the greatest diameter circle at the
bottom and the smallest diameter circle at the top where it is
held.
The top is nearly a node of circular motion while
the bottom is an antinode.
Time how long it takes the slinky to make one revolution. (For
example 1.75 s)
(You can make a more accurate measurement by
timing ten revolutions and then dividing the total time by ten. Start
the timer by counting “start” when the slinky reaches one
place in its circle. Then count 1,2,3,...as it comes back to that
same place, stop the timer when you reach 10.)
(For a qualitative result, you can count the rhythm of the rotation
aloud 1,2,3,4,1,2,3,4 etc.) Find the time for one rotation,
t1
Notice that the motion looks like 1/4 of a sin wave, from a zero at your hand to the first maximum near the floor. So that, if Ls is the length of the slinky then the wavelength of this fundamental motion is 4 Ls. Find the frequency of the fundamental by taking the inverse of the period, f1 = 1/T1.
Move your hand in a faster circle to find the next resonance. The slinky will again have little motion at the top and maximum motion at the bottom, but in between there will be one place closer to the bottom than the top where it will have zero motion, another node.
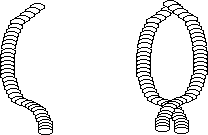
Notice that 3/4 of a wave fits into the length of
the slinky so the wavelength of this harmonic is 4/3 Ls.
Time the period of this rotation. (For example 0.55 s) Find the
frequency of rotation, f3. The
frequency should be should be about 3 times the frequency of the
fundamental.
Notice that the wavelength of the harmonic is 1/3 the wavelength of the fundamental and that the period is also 1/3 of the period of the fundamental.
Qualitatively, you can also count the rhythm of the harmonic. To compare with the fundamental count 1,2,1, 1,2,2, 1,2,3 the rhythm of every third count should be close to the rhythm of the fundamental.
Move your hand faster still and find the next resonance.
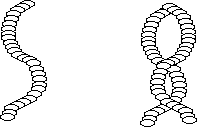
This one will have a node at the top and two other
nodes. Notice that 5/4 of a wave fits into the length of the slinky.
So that the wavelength of this harmonic is 1/5 the wavelength of the
fundamental.
Time the rotation of this harmonic, (for example 0.34 s) the
frequency of this harmonic should be 5 times that of the
fundamental.
What’s going on?
When the slinky’s motion is greatest for the
smallest motion of your hand you have found the resonant frequency of
one of the motions of the revolving slinky.
The resonant frequencies of a slinky with a node at one end and an
antinode at the other are similar to those of a tube with one open
and one closed end. The fundamental has a basic frequency
f0 and the harmonics have odd
multiples of this frequency, 3f0,
5f0, and so on.
The waves on the slinky seem to bunch up at the bottom. The wavelength of waves near the bottom is shorter. This is because the top of the slinky is supporting the entire weight of the slinky below it and so is under high tension. The tension results in a higher speed of waves in the slinky at the top and the higher speed produces a longer wavelength. Conversely at the bottom the slinky is under less tension and so waves travel through it more slowly resulting in a shorter wavelength.
Going Further
Time the up and down bouncing of the slinky
|
Scientific Explorations with Paul Doherty |
|
25 May 2000 |