Strike an aluminum rod and listen to it sing

Strike an aluminum rod and listen to it sing

Materials
A solid aluminum rod 1.2 to 1.6 meters long and 1 cm in
diameter
A hammer, mallet or wooden dowel.
a meter, or two, of fishing line (20 pound test, 10 Kg, or
stronger)
optional
aluminum rods of varying lengths and diameters.
stopwatch
Construction
Make marks along the rod at points 1/2, 1/3, 1/4,1/6, and 1/8 of
the length of the rod from one end.
Make one mark 1/4 of the way from the other end and another 1/6.
To do and Notice
(This is a good activity to do outdoors.)
Activity 1, listening to the rod.
Tap the end of the rod with a hammer while holding the rod at the
1/2 point i.e. at the center
(To find the center balance the rod on your finger.)
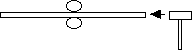
The rod sings two notes.
The lower pitch note may be hard to hear, it dies away more rapidly
than the higher note.
The higher pitch note goes on ringing for a long time, over a minute,
it has a very pure sound.
It has one frequency, the fundamental frequency of longitudinal
motion of the bar.
The note played by the bar is said to have a long
sustain.
With time, the organized motion of the atoms of the rod which we hear
as sound turns into the disorganized motion of thermal energy,
warming the rod imperceptibly.
Some energy goes into sound in the air.
Different materials have different rates at which organized motion
is turned into heat.
Aluminum bars ring for a long time.
Steel bars ring for a shorter time and lead bars ring for a shorter
time still.
Tap the end of the bar on its side (hit it downward).
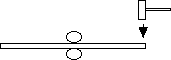
Notice that the lower note is louder than before.
Even in this case, the lower note eventually goes away, and the high
note remains.
Hitting the bar straight into the end makes the bar vibrate along
its length, the resulting vibrations are called longitudinal
vibrations they make the high note that you hear.
Hitting the bar sideways makes it vibrate side-to-side, these are
called transverse vibrations they make the lower note you hear.
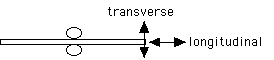
Exploring the pattern of motion of the bar
Do the following then do each of the activities below. Re-strike the bar before each activity.
Hold the bar in the center between two fingers.
Strike it on its end with the hammer to create a longitudinal
vibration, that is, knock the hammer straight into its end.
1. Pinch the end of the bar between the fingers of your free
hand.
Notice that the sound dies away quickly.
2. Pinch the bar between your fingers at a point one inch from the
center.
The sound goes away very slowly
3. Pinch the rod half way from the center to the end.
The sounds goes away moderately quickly.
You can map out the motion of the rod with your fingers. Your
fingers damp out the motion of the rod which makes the sound, i.e.
your finger pads turn the vibrations of the rod into heat.
When you grab the rod where there is a great deal of motion the sound
goes away rapidly.
When you grab the rod at a point where there is little motion the
sound decays slowly.
To quantify the motion, you can use the stopwatch to time how long it
takes for the sound to disappear.
If you plot the motion of the rod versus the position along the rod you get a rough sinusoid.
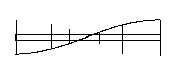
The motion is standardly turned sideways for the
plot.
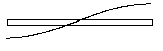
Usually, only one extreme of the motion is
plotted.
The point where you hold the rod, e.g. at the center, is a point with no motion called a node.
One interesting thing to notice is that if you hit the rod at one
end, there is vibration at the other end.
The motion is conveyed past the node where you hold the rod. The lack
of motion at the node only occurs after the first wave passes through
the node, reflects off the far end and returns to the node to cancel
the next incoming wave.
Different patterns of rod vibration
Hold the rod at the 1/4 mark, it will of necessity hang
vertically, strike it straight down on the top end.
Notice the rod makes a higher pitched note.

Hold the rod 1/4 of the way from one end and strike it on the
end.
Map out the motion of the rod by pinching it between your
fingers.
Notice again that the ends of the rod are moving. However, in this
note the metal at the 1/2 way mark is also moving. Perhaps
surprisingly, a point a quarter of the way from the far end is not
moving. This point is another node, a point of no motion.
This higher pitch note has two nodes.
Ask a musician to compare the pitches of this note with that of the bar held in its center. The two notes differ by an octave. The pitch of the bar with nodes 1/4 of the way from one end is twice that of the rod with the node in the center. This vibration is the second harmonic of longitudinal motion. (You can also use a frequency meter/)
Hold the rod at the 1/3 mark, hit the end.
There is no ringing tone. (If there is, then you are listening to a
harmonic of transverse motion.)
There is no pattern of longitudinal motion of the rod which has a
node at 1/3 the length of the rod from the end. There is no way to
draw a uniform sine wave with a maximum at each end of the bar and a
node 1/3 of the way from one end of the bar.
Hold the rod at a point 1/6 of the way from one end. Strike the
end.
The rod will sing with a high pitch (3/2 the frequency of the bar
with nodes 1/4 of the way from the end, i.e. its frequency is higher
by a musical fifth.)
Investigate the pattern of motion of the bar.
There are nodes at the center of the bar and 1/6 of the way from each
end
Investigate other positions at which you hold the rod.
The rod rings with longitudinal motion only when you hold it at
points 1/2,1/4,1/6,1/8 ...1/2n from one end.
A warning about transverse wave patterns
Unfortunately, the rod will ring in transverse oscillation with
nodal points which do not follow the same simple relationship as the
longitudinal waves. In particular, the frequencies of the
longitudinal vibrations we have been examining follow a harmonic
series with a fundamental frequency and integral multiples of that
frequency: f, 2f,3f etc.
The transverse waves do not follow this harmonic relationship, i.e.
the shape of the bent bar is not a uniform sinewave. This means the
rod will ring with lower pitched notes when held at points which do
not fit this simple rule of the harmonic series.
More patterns
Hang the center of the bar from a string. Strike the end of the bar.
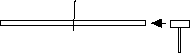
You will hear many frequencies at the same time.
You are hearing many harmonics.
Grab the bar at the center and all of the harmonics which do not have
nodes at the center will vanish. For example both the 1/2
(fundamental) and 1/6 notes will ring. Pinch it also at the 1/6 mark
and the fundamental note will die away while the note with node at
the 1/6 point will ring on.
Extensions, other activities using the bar
Transverse vibrations
For a bar of length L:
Call the frequency of the fundamental of transverse motion
f1.
The wavelength of fundamental is 1.330 L so there are nodes
located 0.224 L from each end of bar.
The family of harmonics for transverse motion are given in the following table.
Harmonic Frequency of harmonic Location of nodes from end
|
Harmonic |
Frequency |
node 1 from each end |
node 2 |
node 3 |
|
1 |
f1 |
0.224 L |
||
|
2 |
2.756 f1 |
0.132 L |
0.5 L |
|
|
3 |
5.404 f1 |
0.094 L |
0.356 L |
|
|
4 |
8.933 f1 |
0.073 L |
0.277 L |
0.500 L |
Notice that the second harmonic has a node at the center. So when we hold the rod at the center we hear the second harmonic of transverse motion and the fundamental of longitudinal motion.
Notice that the third harmonic of transverse vibration has a node near a point 1/3 of the way from the end of the bar, i.e. at 0.356.
Try bars with different diameters. The frequencies of the longitudinal waves are independent of the diameter of the bar, while the frequencies of the transverse wave strongly depend on the diameter. Bars with larger diameters have higher transverse frequencies.
Math Root
The Speed of sound for longitudinal waves is (E/r)0.5
so the fundamental frequency is:
f1L = (E/r)0.5/2L
Where E is the young's modulus for aluminum and
r is the density.
For a cylindrical bar of radius a the fundamental frequency of transverse motion is
f1T = pi*K/8L2(E/r)0.5
in terms of the longitudinal fundamental this becomes
f1T = 3.0112 (pi*/8)
(a/L) f1L
evaluating terms for a 1.4 meter long cylindrical rod 1 cm in
diameter
f1T = 0.012
f1L
The fundamental transverse frequency of bars like the ones we use is 1/80 of the longitudinal fundamental. A much lower frequency.
Going Further
Have students stand in a circle around the bar. Hold the bar in the center and strike it at one end to make it ring. Spin around while holding the ringing bar. While the person holding the bar will hear no change in the frequency of the bar, those standing around the circle will hear the bar change pitch as it passes them. This is a Doppler shift.
Look at the frequency of the bar with an oscilloscope. Measure the
wavelength of a sound wave on the bar with your fingers. Measure the
frequency with a frequency meter or an oscilloscope. Combine the two
measurements to get the speed of sound in aluminum. v = Lf.
Which is over 5,000 m/s.
Look at the sound level produced by the bar with a decibel meter, from Radio Shack. Hold the meter at one end of the bar and time how long it takes for the sound to decay from 60 decibels to 50 decibels as you pinch the bar in different places.
Use the Radio-Shack Decibel meter to measure the loudness of the sound emitted by the bar. Notice that for longitudinal motion, the loudness increases as you approach the ends of the bar. Notice also that loudness decreases with time. The decay of energy with time is exponential. That is it takes the same amount of lime to decay from an initial sound intensity of 1 to an intensity 1/10 as big as it does to decay from 1/10 to 1/100. This means on the decibel scale that the time it takes the sound to decay from 90 dB to 80 dB is the same as the time it takes to decay from 80 dB to 70 dB. Since on the decibel scale subtracting 10 decibels is the same as multiplying by 1/10.
There is no motion at the nodes because standing waves are set up on the bar. Standing waves are produced by the sum of 2 waves moving in opposite directions. The far end of the bar oscillates when you strike the near end because the first sound wave to traverse the bar is a traveling wave. When this wave reflects back through itself it produces a standing wave. and no motion at the node. The presence of damping fingers at the node does not remove much energy from the first traveling wave as it goes by.
|
Scientific Explorations with Paul Doherty |
|
25 May 2000 |