Math Root
Goldilocks found three pinhole cameras, one had a pinhole that was too big...
Introduction
A large pinhole will let in a lot of light but will make a blurry image. As the pinhole gets smaller the image gets dimmer and sharper until at some size, a smaller pinhole makes the image blurrier. The extra blur from a small pinhole is due to diffraction.
Calculation
We can calculate the size of a pinhole that will produce the sharpest image.
Consider a point of light at a great distance from your pinhole camera.
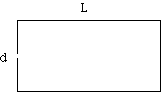
The camera has a length L and a pinhole diameter, d.

What is the best size for the pinhole? That is the pinhole size that makes the sharpest image?
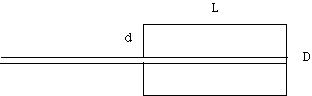
The pinhole allows the rays to hit the film in a circle of diameter, D.
There are two contributions to the blur of the image.
The size of the hole itself allows the parallel rays to hit the film in a circle of diameter d independent of the length of the camera, L.
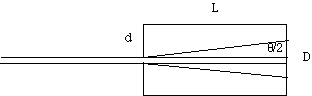
Light diffracts as it passes through the pinhole. The angle of the diffracted beam produced by an infinite slit of width d is approximately
q = 2*l/d
Math Mulch where did this equation come from?
Where q is the angle of the beam divergence in radians. (The angle is measured from the first minimum on one side of the beam to the first minimum on the other.)
and l is the wavelength of light, 5 x 10-7 m.
Then D = q *L = 2*l*L/d
The total blur is the sum of these two:
D = d +2* l*L/d
calculate dD/dd = 0 to find the minimum blur.
dD/dd = 1 - 2*l*L*d-2 = 0
2*l*L*d-2 = 1
d = ( 2*l*L )0.5
with
l = 5 x 10-7 m and L = 0.05 m
d =0.22 mm
A more accurate value for the angle of the diffracted beam for a circular aperture is
q = 1.22 * 2*l/d
Math Mulch where did the 1.22 come from?
so the exact equation for the sharpest pinhole diameter is:
which makes the answer for an L = 5 cm long camera.
d = 0.25 mm
The diameter of the pinhole increases proportional to the square root of the distance from the pinhole to the screen.
The angular diameter of the beam from an infinitely long slit of width d
is sin q = l/d
for small angles we make the approximation sin q = q
and get q = l/d
Where did the 1.22 come from?
The diffraction pattern from a circular aperture produces a beam whose shape is described by a bessel function. The angular diameter of the bessel function measured from the minimum on one side of the center to the minimum on the other side involves an integral over the area of the circular aperture which produces the bessel function and the factor of 1.22.
|
|
|
22 May 2000 |