Interference colors in a soap film
Introduction
Here is a model of wave addition which will guide you in exploring the colors of light reflected by soap bubbles.
Material
3x5 cards at least 24
4x6 or 5x7 cards
masking tape and transparent tape
marking pens, blue and red
optional, acetate transparencies
Assembly
Use a blue pen to draw a single sinewave on twenty-four 3x5 cards. The wave should start at the left center of the card and go up to a maximum.
Flip the cards over top-to-bottom and draw a wave on the back which starts down from the center of the left edge. (If you hold the card up to a light the wave on the front and the wave on the back will coincide.)
Use a red pen to draw similar waves on the larger cards.
Tape the cards together in rows of 8 cards.
Optional Acetate waves:
Cut the acetate sheets into 4 long strips (11 inches long and 2.1 inches wide)
Draw two red sinewaves along the 11 inch length of 8 acetate strips.
Draw 4 blue sinewaves along the 11 inch length of 8 acetate strips.
Use the transparent tape to tape the strips together.
Tape 4 strips together so that their waves match up into one long wave.
To Do and Notice
The colors of soap bubbles.
Start using the smaller, blue cards.
Make two parallel lines with masking tape on the floor.
Make the lines one blue wavelength apart,(For index cards 5 inches or 12.5 cm, for acetate strips 2.75 inches or 6.5 cm)
Start two waves, together on the left of the soap film.
Adjust their position so that they strike the soap film surfaces at the maximum of each wave.
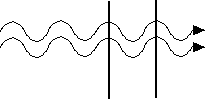
The reflection from the back of the soap film can be found by simply folding the wave back on itself along the line representing the back of the bubble. The drawing on the back of the index cards then accurately shows the reflected wave. When you do this the outgoing and incoming wave lay exactly on top of each other. (The exact alignment of incoming and outgoing waves is only true when you position the maximum or a minimum at the reflecting surface.)
When a light wave reflects as it goes from a high speed of light material (air) to a lower speed of light material (soap) the wave flips over. To make the beam of light reflected by the first surface flip over, flip the wave about a horizontal axis (top-to-bottom) so that the maximum becomes a minimum, then fold the wave back on itself along the line representing the front surface of the soap film.
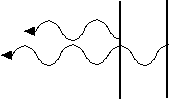
The reflected waves from the two surfaces are out of phase when they combine and so cancel.
What’s Going On?
There are two contributions to the phase of the reflected waves from the two surfaces of soap films: the wave flips over as it is reflected off the front surface, that is, as light goes from air to soap, and the extra path length traveled by the wave which goes into the soap then reflects off the back surface and returns to the front. When the soap film is thin, there is little contribution from the extra path length and so the waves add out-of-phase and cancel. There is no reflection from such a thin bubble. Since the colors of bubbles are usually viewed against a black background, this thin bubble with no reflection is called “black” even though it is actually transparent.
It’s more complicated than that.
The wavelength of the light actually changes when it enters the soap film. In our model we have not added this additional complication. Think of the thickness of the soap film in terms of the number of wavelengths measured in the soap film. Since the index of refraction of soap is a little higher than that of water, for soap use n = 1.4, then the wavelength of light in soap is the wavelength in air divided by 1.4.
To Do and Notice
Explore what happens when the soap films are very close together. One of the waves flips over, and there is no additional phase shift because there is no extra path length. the waves cancel.
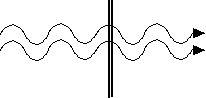
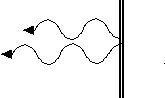
To Do and Notice
Explore what happens when the soap films are 1/2 wavelength apart so that the front surface is at a wave maximum while the back is at a minimum. The extra pathlength is one full wave, so the waves cancel.
So far, it looks like light is never reflected from soap films. However, try a soap film thickness of 1/4 wavelength. Align the front of the soap film with the maximum of the waves the the back will then be at a zero crossing. Flip over the wave reflected from the front. Fold back on itself the wave from the back. This reflected wave will add with the reflection from the front surface in-phase and make a stronger reflection.
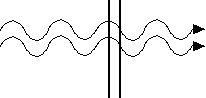
What’s Going On?
The reflection from the front surface is flipped over, the reflection from the back travels a half wavelength extra so it arrives at the front surface with the same phase and so adds to the front surface reflection.
To Do and Notice
Explore soap films which are 1/4 and 1/2 of a blue wavelength in thickness a second time using red light. Notice that where the soap film reflections cancel for blue light they add for red light and vice versa.
Further Explorations
To Do and Notice
To explore any thickness of soap film use the following recipe.
Always arrange the incoming light so that a maximum of each wave is at the front surface of the soap film.
Flip over top to bottom one of the waves to represent inversion when it reflects off the front surface.
Fold the wave that hits the back surface back on itself.
Add the two waves together as they exit the film.
What's Going On?
When the wave reflects off the back surface without inversion what reflects off is what has just hit the surface. If a downward portion of the sinewave has just hit the surface then a downward portion should be what is reflected. This is simply accomplished by folding the wave back on itself.
Etc
Soap bubbles have two different stable thicknesses which look black. The thicker of these is called the common black film, it is 30 nm thick &emdash; about 300 atoms thick or 10 soap molecules or 1/20 the wavelength of light. The thinner film is called the Newton black film, it is about 6 nm thick,1/100 the wavelength of light, or two soap molecules, and is much more transparent, i.e. much “blacker.”
Math Root
One complete sine wave has a phase associated with it of 2p radians.
The phase difference between two waves which are in-phase is 0, 2p, or any even multiple of p radians.
Waves which completely cancel have a phase difference of p, 3p, or any odd multiple of p radians.
Waves with in-between phase differences add together with amplitudes between those of completely in-phase and completely out-of-phase.
Reflections from the surfaces of bubbles which are thin compared to a wavelength of light have a phase difference of p from the flipping over of the reflection from the front surface, there is little phase difference from the extra path length.
Reflections from bubbles one half-wavelength thick have a total phase difference of 3p; one p from the flipping over at the front surface, and two more from the extra path length which is two half waves or one complete wave.
Reflections from bubbles which are 1/4 wavelength thick have a total phase difference of 2p, one p from the flipping over at the front surface, the second from the extra half wave the other reflection travels through the film and back.
Math Root 2
The fraction of the energy of the light reflected at the first surface is 4% of the incoming beam (when the light comes into the soap film nearly perpendicular). We can measure this reflection from single surface of soap, such as occur at the top of vats of soap.
The energy reflected is the square of the amplitude of the light wave. So if the light wave has an amplitude of 1.0 then the reflected light has an amplitude of 0.2. The intensity of the reflected light is the amplitude squared or 0.22 = 0.04.
To find the intensity of the reflected light we must add the amplitudes of the waves we have been modeling and then square the results. So when the light reflects in phase from two surfaces we add the two amplitudes, 0.2 + 0.2 = 0.4 and then square to find that 0.16 or 16% of the incident light is reflected by a two surface soap film which is 1/4 wavelength thick.
Many people expect that a two surface soap film will reflect twice as much as a single soap film or 8%, when the reflected waves have a constant phase difference, this expectation is incorrect. (The constant phase difference comes about when the soap film is illuminated with coherent laser light.)
First you add the reflected amplitudes and then you square the result to find the resulting intensity of the scattered light.