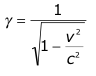
Relativity
Teacher Institute Explores the zeroth level knowledge you need to appreciate relativity and some of the more advanced modern topics that can be explored with hands-on materials.
Einstein thought that the most important parts of relativity were the things that stayed constant from one reference frame to another.
Perhaps it should be called the theory of invariants.
The most important invariant is one of the fundamental postulates of relativity, the speed of light is the same in all reference frames.
Check out the exploratorium web pages on relativity. Here is the first one Thinking like Einstein: http://www.exploratorium.edu/relativity/einstein.html
Einstein had two basic postulates of relativity:
1.) The speed of light in a vacuum is the same for all observers. http://www.exploratorium.edu/relativity/einstein_speed.html
2.)The laws of physics are the same as long as you travel at a constant speed. http://www.exploratorium.edu/relativity/einstein_laws.html
Postulate 2 was a great addition to physics: We already postulated that the laws of physics should be the same when:
1. Experiments are conducted in different positions
2. Experiments are conducted at different times
3. Experiments are conducted with the apparatus facing different directions
Einstein's postulate added 4.) experimental results are the same at all different constant speeds.
If you drop a ball in a constantly moving airplane it falls as it would on earth.
This postulate means you cannot do an experiment in a closed room to detect whether the room is moving in a straight line at a constant speed.
What this really means is that in a frame of reference all clocks must run at the same rate,
because if two clocks ran at different rates as a function of speed then you could use the difference to detect your motion.
This is why we will use the simple light clock. All clocks run the same as the light clock and it is an easy clock to understand.
Question, If we cannot detect uniform motion, how can we know the earth is moving toward "The Great Attractor" the Centaurus supercluster of galaxies at a speed of 600km/s.
Answer. We look outside the box and see the superclusters motion relative to us.
Postulate 1. shows that motion near the speed of light does not obey the rules we know and love at slow speeds.
Throw a baseball at 100 km/hr. Now throw the baseball forward from a truck moving 100 km/hr on the truck you see the baseball move forward at 100 km/hr
A viewer on the ground beside the truck sees the baseball traveling 200 km per hour. (What does the observer see if the baseball is thrown backward?)
Light moves at the speed of light c. Shine light from the headlights of a fast truck traveling 0.99C and a person on the truck sees the light leave at c.
A person on the ground beside the truck also sees it pass at c.
This was experimentally measured by A. A. Michelson and E. W. Morly in 1887. Using the earth's orbital velocity as their fast truck. The earth orbits at 30 km/s 3*10^5 m/c or about 0.001c
Space and Time
Since Ole Roemer's time, 1676, we've known that space and time are coupled. http://en.wikipedia.org/wiki/Ole_Rˆ½mer
Looking out in space is looking back in time.
Because light travels at a finite speed of light.
We see the moon as it was a little over a second ago, because light from the moon takes over a second to travel to us.
| Object | Time ago |
| Student 10 ft. away | 10 ns |
| Moon | 1.3 s |
| Sun | 8.5 s |
| nearest star | 4 years |
| Andromeda galaxy | 2 million years |
| Big Bang | 13.7 billion years |
It is interesting that astronomers measure distance in a unit of time, 4 light years, the distance light travels in 4 years.
The speed of light c becomes a conversion factor turning seconds into meters d = ct, how long is a light year d = 3 * 10^8 m/s * 3 * 10^7 s = 9 * 10^15 m or about 10^16 m
But in relativity space and time are coupled even more into spacetime.
So when you see the moon you see it where it was a second ago. Since you know how the moon is moving you can calculate where it was a second ago. Or if you filled space with recorders then you could collect the signals from all the recorders, in particular those near the moon and find out where the moon actually was not where it "appeared" to be to your eye.
The simple calculations of relativity do not reveal how an object in motion appears to an observer or a camera, the calculations show how the object will be measured in a space full of sensors after all the data from the sensors is gathered in one place and analyzed.
It's not how it looks it's how it's measured.
The answers we get from length contraction and time dilation are not the answers to how something "looks" to one observer.
In everyday slow speed life we obtain a view of the universe through our eyes, this no longer works in relativity.
The travel time for light from different parts of an object can really distort the appearance of the object. The mathematical calculations of how things "appear" are tedious.
So in relativity we speak of measurements not appearances.
Here is a great introduction to appearance versus measurement. From a physicist at U Toronto.
http://faraday.physics.utoronto.ca/PVB/Harrison/SpecRel/Flash/ContractInvisible.html
Frames of Reference
Before you work with relativity you must understand frames of reference.
The great movie "Frames of Reference" is now available free online. http://www.archive.org/details/frames_of_reference
Here are two great activities that requires an ability to shift frames of reference.
Ball Bounce If you drop a tennis ball on top of a basketball the tennis ball will bounce high into the air, understanding the collision requires shifting frames of reference.
Silent Collisions Two magnets can collide in an elastic collision, understanding the result requires shifting frames of reference.
Here is a blank Frames of reference pdf.
Gamma
You'll notice that the term gamma, g, occurs a lot in relativity : where c is the speed of light and v is the velocity of a moving frame of reference.
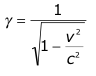
Here is a table of cool values of gamma:
| speed | gamma | 1/gamma |
| 0.1 | 1.005 | 0.995 |
| 0.5 | 1.15 | 0.87 |
| 0.87 | 2 | 0.5 |
| 0.995 | 10 | 0.10 |
| 0.99995 | 100 | 0.01 |
In general for small values of speed, g will be 1 plus half the square of the speed.
Light Clock: Time Dilation
A light clock http://www.exploratorium.edu/relativity/time_math.html
Time dilation http://www.youtube.com/watch?v=KHjpBjgIMVk see a cartoon of the clock in motion.
Time dilation a modern repeat of the actual experiment, Atomic Clocks on a Plane, http://www.youtube.com/watch?v=gdRmCqylsME&feature=related
Animated mathematics http://www.youtube.com/watch?v=W_LFtrWie3g
Make a clock in which a pulse of light travels between two mirrors and ticks each time it hits a mirror.
Light travels at C =3 *10^8 m/s or 300 million meters per second. If you wanted to make the clock tick once a second how far apart should the mirrors be?
That is a mighty big clock. The average distance to the moon is 3.8 x 10^8 m.
The really interesting thing is that the equation for the rate of time passing on a moving clock involves gamma, and if you plot the rate at which a clock ticks versus speed you will see the meaning of the gamma term in relativity: The plot is the arc of a circle.
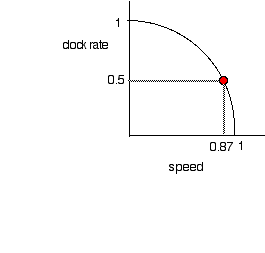
A clock with a period , T of a half second, will have a rate of R = 1/T = 2 times a second or 2 Hz.
Period and time are inversely related.
A clock which you observe moving at 0.87 the speed of light is measured to run at 0.5 times the rate of the same clock at rest.
The period of the clock seen to be moving at 0.87 c doubles For v = 0.87c then g = 2. We call this time dilation.
A human heart beat can be viewed as a clock pulsing about once per second, 1 Hz. A human seen moving at 0.87 c will be seen to have a heart that beats at half the rate, 0.5 Hz, or with a period of once every 2 seconds.
The clock rate is 1 when it runs at the same rate as a clock at rest. The clock rate goes to 0 when it approaches light speed.
The speed is given as the fraction of the speed of light.
Here are some larger versions of the above graph. Time Dilation
Time dilation has been directly measured by taking atomic clocks for rides in airplanes and also by measuring the lifetimes of muons.
Time dilation and muons http://nobelprize.org/educational_games/physics/relativity/transformations-4.html
You can see the tracks made by muons created in the atmosphere and passing through the exploratorium at the Cloud Chamber exhibit.
The derivation of gamma, from the circle above notice that if the speed is v/c and the clock rate is R then from the equation for the unit circle 1 = x^2 + y^2 then
1 = R^2 + (v/c)^2 and so R = (1-v^2/c^2)^0.5 the rate is 1/gamma
Length Contraction
When a rod is measured at rest it has a length L0 called its rest length or its proper length. It is easy to measure the length of a rod on a table. You can measure the location of the front and back of the rod at any time.
When a rod is moving along its length it is harder to measure, since the position of both ends must be measured simultaneously! And people who are moving with respect to each other no longer agree on what is simultaneous. A rod in motion will always be measured to have a length, L, shorter than its rest length.
L = L0/g
Thus a moving rod is measured to have the fraction of its length given by the same circular arc as the clock rate versus speed shown above.
Measure the length of a moving rod. Try to measure the length of a rod moving along a table top.
Morph Yourself Take an image of yourself and adjust its height to give an appropriate length contraction.
There was a young fencer named Fisk
Who's wrist was exceedingly brisk
So fast was his action
the Lorentz Contraction
Shortened his rapier to a disk.
David Harrison U Toronto animation of muons and length contraction http://faraday.physics.utoronto.ca/PVB/Harrison/SpecRel/Flash/LengthContract.html
Lack of simultaneity for two events viewed from reference frames in relative motion. http://faraday.physics.utoronto.ca/PVB/Harrison/SpecRel/Flash/Simultaneity.html
The Twin Paradox http://faraday.physics.utoronto.ca/PVB/Harrison/SpecRel/Flash/TwinParadox.html
Advanced Activities
Light travels in vacuum. So I say "Light is a creature of the vacuum." Paul Doherty
Light speed depends on the dielectric permeability of the vacuum, e0, and the magnetic permeability of the vacuum mo.
c^2 = 1/e0mo
It is not surprising then that as the vacuum of the universe expands light expands with it as illustrated by drawing a wave on a rubber band and stretching the rubber band.
The distance between two places in the vacuum of space is affected by the presence of nearby mass.
Light Falls under gravity, In the curved space exploration above we calculate how far light falls as it crosses a room. When astronomers look out into space they can wee light from distant galaxies curved into rings, arcs and extra images by the gravity of nearby galaxies.
The Elegant Universe, Genral relativity, the speed of gravity.http://www.youtube.com/watch?v=tpbGuuGosAY&NR=1
References:
Was Einstein Right 2nd ed, Clifford Will, the most readable description of the experimental tests of relativity,
http://www.amazon.com/Was-Einstein-Right-2nd-Relativity/dp/0465090869/ref=sr_1_1?ie=UTF8&s=books&qid=1237218161&sr=1-1
It's About Time, A book written to accompany a class on relativity written for high school physics teachers.
http://www.amazon.com/Its-About-Time-Understanding-Relativity/dp/0691122016/ref=sr_1_2?ie=UTF8&s=books&qid=1237489308&sr=1-2
Spacetime Physics, 2nd ed, Edwin Taylor, A book about relativity for college students.
http://www.amazon.com/Spacetime-Physics-Edwin-F-Taylor/dp/0716723271
Hyper physics on Relativity http://hyperphysics.phy-astr.gsu.edu/hbase/relativ/relcon.html#c1
Scientific Explorations with Paul Doherty |
16 March 2009 |