drawingphysics

Drawing Physics

A picture is worth a thousand words. version 5, 1 Mar 93

Paul Doherty

When I encounter a physics problem I almost always begin by reaching for a piece of paper and a pencil to make a drawing. Most of the physicists I know start to solve science problems by making a drawing. Frank Oppenheimer was famous, around the Exploratorium, for creating extremely small drawings&emdash; scientific miniatures), to accompany his solutions to physics problems. When you encounter problems, try making a sketch to help you see the problem, it might lead you to the solution.

Of course making the correct drawing will be most helpful. Let's look at the rules for making four of the most important types of drawings in all of physics.

force isolation drawings,
ray tracing diagrams,
energy diagrams.
and phase diagrams

Scientists have developed formal rules they follow when the make their drawings. Let me introduce you to each of these drawings by using them to solve simple science problems. I'll show you how specific drawings are used to investigate how you feel when you ride a roller coaster, why a magnifying glass sometimes makes upside-down images and sometimes right-side-up, at what temperature water liquid boils, and finally, why what goes up may not necessarily come down.

Force isolation diagrams

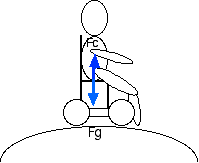
Physicists are often need to predict the motion of an object, predicting motion becomes particularly interesting when they are the moving object. Look at the drawing of a physicist going over the top of a hill in a roller coaster. The sketch becomes a useful tool when forces are added to the drawing. Not just any forces, only forces on the "object," in this case the physicist. After an object is identified and drawn and all of the forces on it are shown then the drawing then becomes a force isolation diagram&emdash; a diagram rooted in the reality of the object, but which also shows the invisible forces.

Forces are shown as arrows&emdash; vectors to a physicist. The length of an arrow is proportional to the strength of the force it represents, the direction shows the direction of the force. The arrows are usually drawn starting at, or at least close to, the place where the force acts on the object. Once they are identified, all of the forces &emdash; arrows &emdash; on an object can be added together to get the bottom line, known as the net force. The net force is the key to understanding the motion of the object. Simply put, if there is a net force then the object is accelerating, or changing its velocity, in the direction of the net force.

In the case of the going-over-the-hill-physicist shown in figure 1 there are two important forces: the downward force of gravity and the upward contact force of the seat. The contact force is smaller than the gravity force, so when they are added together there is a net force and the physicist accelerates down. Indeed, the physicist does follow a downward curving path, a path in which its velocity is continuously changing its direction, a path which shows the acceleration produced by the net force.

The physics explanation seems to go against how I feel as I go over a hill on a coaster. Somehow I feel "lighter," and yet the drawing shows the same force of gravity on me as in figure 2, a drawing of a me on a coaster at rest. Humans cannot directly sense the force of gravity on our bodies. This sounds like heresy. But it is true. What we do feel are the pressures on and compressions of our body produced by the contact forces that keep us from being sucked into the earth by gravity. Skiers buried by avalanches are tumbled about and eventually imprisoned, motionless, compressed by the snow from all sides. Those that survive report that they cannot sense which way is up.

So, while you might say you feel gravity, what you actually feel are the contact forces. The contact force exerted on you by the seat as you ride the coaster over the hill is indeed less.

To Do and Notice, Sit on your hands.

Try riding the coaster while sitting on your hands, your hands will directly feel the changes in the contact force during the ride.

A second diagram will help clarify your feelings as you go over the hill&emdash; a force isolation diagram for your intestines. When the coaster is at rest, your intestines are squeezed between two contact forces, the downward forces from the organs above, like the stomach, and the upward force from the pelvis below. However, as we crest the hill on the coaster, both the downward force from the stomach and the upward force from the pelvis are reduced. (The gravity force on the intestines remains the same of course.) With a reduced compression force the intestines expand, as any coiled spring would, producing strange internal feelings.

As another interesting aside, every atom of the earth pulls gravitationally on every atom of a human bodies. Physicists find that instead of drawing the individual forces on each atom of an object they can replace the many forces by a single force acting at a point called the "center of gravity." The gravity force is drawn downward, or toward the center of the earth from the center of gravity.

(675 words)

possible further drawings:

terminal velocity for a parachutist,

accelerating up in an elevator, and

freefall in orbit.

To do and notice stand on a scale in an elevator, sit on your hands in a rollercoaster, float in a sensory deprivation tank.)

Following the light

Find a magnifying glass and look through it. Distant objects appear upside down and nearby objects look right-side up. How does the lens do that. To figure out how a magnifying lens makes images I immediately draw a ray tracing diagram.

Light spreads out in straight lines from every point on an object. When the spreading light hits the lens, the light bends. A magnifying glass which is thicker in the center than at the edges bends light toward the center of the lens. A human viewing light which has passed through the lens will see the light spreading out from a point which is not located at the position of the original object. The eye and brain sees an image located at the point from which the light rays spread.

Like the force isolation diagram above, the ray tracing diagram mixes drawings of the real lens with abstract drawings of light rays. If you make real rays of light with the sun, a bulb or a laser (photo of light island exhibit) you can follow them to, through, and beyond the lens and observe how they bend. The rays drawn in the ray tracing diagram follow paths which are similar to, but not exactly identical to, the ones followed by real light rays.

The first ray trace shows how a magnifying lens makes an inverted real image of a distant thumb&emdash; one at arms length. To find the image draw the thumb, the lens, and a line representing the axis of the lens. (If the lens were a wheel the axis would be the axle.) Next, mark two special points on the axis, the focal points of the lens. These are the points to which light entering the lens parallel to the axis from either side will be focussed(see To Do and Notice).

To Do and Notice finding the focal points of a lens

To find the location of the focal points of a lens find a distant light source such as a street light, hold the lens between the light and a piece of stiff paper, move the lens back and forth until an image of the light appears on the paper. The image will be located near the focal point, as long as the the light source is more than ten times further from the lens than the image is.

A point on the image will be formed where two lines cross. Luckily, three rays of light can be easily traced through a lens. The first ray passes through the center of the lens, and is known as the chief ray. The chief ray is a straight line, it does not bend. Here we see why the rays in a ray tracing diagram are only approximations to real rays. The real ray which passes through the center of the lens bends as it enters the lens then bends again when it exits. The real ray exits parallel to its entering direction but displaced slightly to the side. The ray tracing diagram we are drawing here assumes that the lens is relatively thin, the jog to the side is small, in a thin lens, and can be ignored.

For the second ray, there are two rays to choose from. One ray called the parallel ray, travels from the object to the lens parallel to the axis of the lens. This ray bends at the lens and passes through the focal point of the lens. The image is located where this parallel ray crosses the chief ray. An alternate choice is the focal ray, which goes from the thumb through the nearby focal point and exits the lens parallel to the axis.

A viewer will see an image thumb located at the point from which the light rays spread, the crossing point of the rays. Notice that the image is inverted. If the thumbs-up sign is being given then the image will be thumbs-down.

The second ray tracing drawing shows what happens when the thumb is brought close to the lens. The light rays exiting the lens never cross, but to a viewer they seem to radiate from an image point on the same side of the lens as the object. Light from the high point of the thumb remains at the high point of the image. Physicists call images formed by light rays which actually cross at the image points, real images, other images are called virtual images.

Thus, simple ray tracing shows why the images made by the lens of a distant object is upside down while the image of a nearby object is right-side up.

(775 words)

Energy diagrams

Often it's simpler to understand motion by looking at energy than it is by looking at the vector forces. For example, the energy diagram of figure x can be used to show why "what goes up doesn't necessarily come down." The curved line shows the amount of energy you have to add to an object to lift it away from the surface of the earth. Near the earth the force of gravity is strong and it takes a great deal of work, i.e. energy, to lift an object one meter. Far from the earth however the force of gravity is weaker and so less energy is required to lift the object the same meter. The work done to lift the object can be recovered by dropping the object, so the object stores the energy when it is in an elevated position, it is said to have potential energy. This figure is a graph of the gravitational potential energy for the earth.

To launch a spacecraft from the surface of the earth, the spacecraft must be given energy, usually by burning rocket fuel. In the first few seconds of flight the rocket gains a little altitude and a lot of speed. So, initially, the work done by the rocket motor goes into speeding up the spacecraft, increasing its energy of motion&emdash;known as kinetic energy. Consider a small sounding rocket like the Scout which is used to launch a spacecraft. When launched by the Scout, spacecraft do not reach orbit, they simply go up and then down. On the way up, the kinetic energy of the Scout decreases as its potential energy increases. Once the rocket gets above the atmosphere, there is no friction, so the kinetic energy is completely converted into potential energy, none is lost as heat. The sum of the kinetic and potential energy is therefore a constant and is shown on the graph as a straight horizontal line. It's easy to read the kinetic energy from the graph, it is the distance from the potential energy curve to the total energy line.

The point where the total energy line crosses the potential energy line is an important point,. Called the turning point, it is the place where the kinetic energy goes to zero. The spacecraft stops at the turning point, then begins its fall back to earth. It loses potential energy and gains kinetic as it falls until it collides with the atmosphere or the surface.

The gravitational potential energy curve for a planet levels out at great distances from the planet. This is important because it means that if a spacecraft is given enough kinetic energy then the total energy line will always be above the potential energy line. This means that the spacecraft will never reach a turning point, it will keep moving away from the earth forever. The spacecraft then is said to have escaped the earth, it has escape energy.

The speed necessary to give a spacecraft escape energy is known as escape velocity. From the surface of the earth escape velocity is 25,000 miles per hour (11 km/s). When spacecraft go to Mars, they must have speeds greater than escape velocity as they leave the earth.

It is also interesting to note that an object dropped from rest at a great distance will turn its initial potential energy into kinetic energy and strike the earth with escape velocity. The kinetic energy of such an object goes into light and heat when it hits the atmosphere, it becomes a meteor. If it survives unvaporized to strike the earth it delivers its energy to the surface carving a crater. At escape velocity a one kilogram rock (which weighs about two-and-a-half pounds on earth) has 60 megajoules of kinetic energy. This is 4 times the energy released by a kilogram of TNT.

More examples of using energy diagrams

escape velocity from Phobos = fast pitched baseball speed.

(618 words)

So with these three example of drawings I hope I've helped you to see how physicists use drawings to solve problems. Remember though that just as it takes a artists time to master drawing techniques so too does it take time for scientists to become proficient at making useful drawings. So the next time you have a science problem to solve start by making a drawing, if you still can't solve the problem take a tip from my friend Will Crowther, who suggests that you behave quite the opposite of Frank Oppenheimer, and draw the drawing again, bigger.